Les premières découvertes
Étant donné qu'il n'y a plus guère de nouvelles
informations sur le météore d'Espagne et qu'il y a
pourtant sûrement pas mal de choses à dire, je me suis
décidé à pousser un peu plus loin mes
hypothèses (à défaut d'investigations), pour
essayer d'estimer vraiment où les météorites
avaient pu tomber... Parce que des météorites, il y en a
déjà un certain nombre, et d'autres restent
sûrement à découvrir !
Quelques jours après la chute, un journaliste du nom d'Abel
Tarilonte, qui se trouvait dans la région et avait
assisté au phénomène, a pu retrouver deux petits
fragments, pesant 20 et 40 grammes. Ces fragments ont été
examinés par Javier García Guinea, professeur de
minéralogie du Musée national des sciences naturelles de
Madrid, qui a confirmé qu'il s'agissait bien de
météorites, et que leur chute était très
récente d'après le peu d'oxydation de leur surface.
D'après les premiers résultats, il s'agirait d'une
chondrite ordinaire, composée essentiellement d'olivine
(cristal, silicate de fer et de magnésium), de troilite (sulfure
de fer), de métaux (fer, nickel et chrome) et de roches...
Il s'agit d'une classe de météorites très
ordinaire, et devant le peu d'enthousiasme provoqué par sa
découverte, Tarilonte a décidé d'en faire cadeau
aux chercheurs.
Le lieu précis de la découverte n'a pas été
révélé, il se situerait dans les « montagnes
de Palencia », lesquelles couvrent une grande surface.
Depuis, neuf autres pierres ont été découvertes
par des chercheurs du SPMN (qui a annoncé la nouvelle
sur son site
le 4 février) et le Musée national des sciences
naturelles. Le lieu, « une zone très précise du nord
de la Palencia », est aussi gardé secret pour éviter
les recherches « sauvages »...
Le SPMN espère aussi toujours disposer d'informations
suffisamment précises pour estimer non seulement la trajectoire
exacte, mais aussi l'orbite de l'objet avant qu'il ne rencontre la
Terre. Il a besoin pour cela d'un maximum d'enregistrements
(photos ou vidéos) du passage du phénomène, et
pour en recueillir encore ce groupe a lancé
un concours récompensant la meilleure vidéo et la meilleure photographie du phénomène.
Essayons donc de préciser un peu mieux que nous ne l'avons
déjà fait le lieu de chute. En suivant notre trajectoire
estimée, laquelle ne doit pas être trop
éloignée de la vérité, on remarque qu'une
chaîne de montagnes, les monts Cantabriques, se trouve sur le
chemin de l'objet, et sans doute pas très loin du point de chute
en tenant compte du freinage atmosphérique. Il y a dès
lors une forte probabilité que l'objet, ou plutôt les
objets qui ont survécu à la fragmentation, aient
terminé leur course sur le flanc de ces montagnes. Et il s'agit
bien des seules montagnes présentes dans la province de
Palencia, tout à fait au nord. On peut donc supposer que s'il a
fallu autant de temps pour retrouver aussi peu de
météorites, et si les recherches continuent après
un mois et demi, c'est parce que la zone est couverte de neige. Dans ce
cas, il faudra sans doute attendre le printemps pour qu'elle soit
vraiment ratissée.
Parlons d'atmosphère
Jusqu'à présent, nous avions négligé dans
nos calculs l'influence de l'atmosphère terrestre, laquelle
n'intervient que dans la dernière partie de la trajectoire. Il
est temps de la prendre en compte, ce qui nous permettra d'effectuer
quelques révisions.
La force exercée par l'atmosphère sur un objet en
déplacement est proportionnelle à la densité de
l'atmosphère, à la section maximale de l'objet
perpendiculaire au déplacement, ou surface frontale, au
carré de sa vitesse, et à un coefficient dépendant
de la forme plus ou moins effilée de l'objet : le coefficient de
traînée ou « coefficient de pénétration
dans l'air ».
On écrit plus précisément :
F = 1/2 C
D.ρ.S.V
2.
ρ (rhô) est la densité de l'atmosphère, ou
plutôt sa masse spécifique (c'est la même chose mais
en unités différentes : la masse spécifique est la
masse d'un volume unitaire, la densité est la masse
spécifique comparée à celle de l'eau), et C
D
est le coefficient de traînée... Pour un objet de forme
à peu près quelconque, il est à peu près
égal à 2,5 ; on cherche à le
réduire dans le cas des véhicules en déplacement
dans l'air, mais ça n'est pas ce qui nous intéresse ici.
Le reste doit bien sûr être exprimé dans un
système d'unités cohérent, soit pour le
système international des kilogrammes par mètre cube pour
la masse spécifique, des mètres carrés pour la
surface frontale, et des mètres par seconde pour la vitesse,
avec un résultat en newtons.
Ce qui nous intéresse n'est pas la force mais plutôt
l'accélération, que l'on obtient en divisant la force par
la masse de l'objet (et en ajoutant par convention un signe moins pour
signifier que c'est une décélération). Bien
sûr, la masse sera donnée en kilogrammes, et le
résultat pour l'accélération sera en m/s
2.
On voit que la seule variable dépendant du milieu
extérieur est la masse spécifique de l'atmosphère,
déterminée par l'altitude. Au sol, elle est égale
à 1,293 kg/m
3,
mais elle est divisée par e, la
base des des logarithmes népériens (2,718), tous les
8 km. C'est ce que l'on appelle l'échelle de hauteur de
l'atmosphère. On pourrait très bien l'exprimer dans une
autre base logarithmique, par une conversion très simple :
si vous voulez par exemple connaître l'échelle de hauteur
en
base 10 (pour savoir de combien on doit s'élever pour que
l'atmosphère soit dix fois moins dense), vous devez multiplier
les 8 km en base e par dix et diviser par e ; vous obtenez
29,5 km. Les
logarithmes népériens sont simplement les plus
« naturels » (on les qualifie aussi ainsi), parce que la
pente de la courbe logarithmique est alors égale au logarithme
lui-même (si vous ne comprenez pas, ça n'a aucune
importance).
La densité de l'atmosphère à une altitude
donnée (h, en kilomètres) sera donc égale à :
ρ
0/e
h/8.
Donc, un météoroïde sera de plus en plus
freiné à mesure qu'il s'enfoncera dans
l'atmosphère. La perte de vitesse se traduira par un
échauffement (proportionnel à la perte d'énergie
cinétique, égale à m.v
2/2) qui fera
fondre ou évaporer l'objet en surface... On appelle cette perte
de matière l'ablation. Plus l'objet est petit, plus le freinage
auquel il est soumis est important, et plus l'ablation est rapide. La
masse critique pour qu'une partie de l'objet puisse atteindre le sol
dépend bien sûr de sa résistance (à la
chaleur aussi bien qu'aux chocs), de sa vitesse initiale et de l'angle
de pénétration dans l'atmosphère, mais elle est de
l'ordre d'une tonne...
Un objet suffisamment gros et compact, de l'ordre d'au moins cent
tonnes, peut atteindre le sol entier et sans avoir beaucoup perdu de sa
matière ni de sa vitesse ; dans ce cas l'impact forme un
véritable cratère, et il n'est pas rare qu'on ne trouve
pas non plus de météorite parce que l'objet est
complètement pulvérisé par le choc. De tels
impacts sont heureusement rares.
Un objet de taille intermédiaire sera suffisamment ralenti pour
atteindre le sol sans trop de dégâts (en tout cas si
personne ne le reçoit sur la tête, mais la
probabilité est suffisamment faible pour que les
météorites n'aient fait aucune victime attestée
dans l'histoire récente), et assez discrètement
puisqu'ayant perdu pratiquement toute son énergie
cinétique il ne sera plus échauffé et ne sera donc
plus lumineux (c'est pour cela qu'il est rarissime que les
météorites provoquent des incendies)...
Il est fréquent aussi qu'un de ces objets de taille
intermédiaire subisse lorsqu'il pénètre dans la
basse atmosphère (à une altitude de l'ordre de 30
à 50 km, quand la décélération est
maximale) une décélération tellement importante
(plusieurs centaines de g) qu'il se fragmente, provoquant comme une
explosion de lumière puisque les fragments beaucoup plus petits
que le corps d'origine sont alors soumis à une
décélération encore supérieure. La
fragmentation produit une sorte de réaction en chaîne,
totalement destructive ou ne laissant subsister que quelques fragments
suffisamment gros et solides pour avoir résisté au choc.
Ces fragments subissent alors une décélération
rapide, et achèvent leur course non loin du lieu de la
fragmentation.
C'est ce qui s'est passé avec notre météore,
puisqu'on voit cette « explosion » brutale sur la
vidéo.
Application à notre météore
Voyons maintenant si nos précédentes estimations
concernant le météore restent vraisemblables lorsqu'on
fait intervenir le freinage atmosphérique.
Nous avons vu que la masse de l'objet devait être d'environ 10
tonnes (cette estimation se fait d'après la luminosité et
la distance).
On sait aussi par les quelques fragments retrouvés qu'il s'agit
d'une météorite courante, de type chondrite, dont la
densité est de l'ordre de 3,5. Celle-ci contiendrait toutefois
d'après les premières déclarations concernant les
analyses une quantité inhabituelle de fer dont la densité
est nettement supérieure, on peut donc arrondir à 4
(ça ne changera de toute façon pas grand-chose)... Pour
une masse de dix tonnes, le volume sera donc de 2,5 m
3.
Et avec le volume, on peut calculer le rayon, puis la surface frontale
(en assimilant l'objet à une sphère) :
r
3 = 3V/4π ⇒ r = 0,842 m.
S = π.r
2 = 2,227 m
2.
Nous avions trouvé raisonnable de considérer qu'au point
de référence, lorsqu'il était filmé,
l'objet se trouvait à une altitude de 18 km, et filait à
une vitesse théorique (sans tenir compte du freinage
déjà subi) de 18 km/s. Cette vitesse théorique
aboutissait à une vitesse angulaire théorique en azimut
sur la vidéo de 11,9°, contre 9° mesurés. La
vitesse réelle aurait donc été égale
à 18000×9/11,9 = 13600 m/s.
La masse spécifique de l'atmosphère est, à cette altitude :
1,293/e
18/8 = 0,136 kg/m
3.
On trouve donc pour l'accélération :
-1/2 C
D.ρ.S.V
2/M = -1/2×2,5×0,136×2,227×13600
2/10000 = 7014 m/s
2...
Il est assez peu vraisemblable que l'objet ait perdu autant de vitesse
en une seule seconde alors que la durée de la visibilité
sur la vidéo est de 1,4 s, et qu'il n'ait perdu avant cela
que 4 km/s alors que l'altitude n'aurait pas beaucoup varié
en
plusieurs secondes...
Visiblement, un tel freinage serait un peu trop brutal pour que nos
estimations soient cohérentes... Voyons ce que l'on pourrait
corriger :
— La masse : un objet plus massif ralentit moins... Toutefois, le
freinage par l'atmosphère est proportionnel au rapport
surface/masse, donc inversement proportionnel au rayon. Et le rayon
variant en fonction du cube de la masse, il faut multiplier la masse
par 8 pour que le freinage atmosphérique soit divisé par
2... Mais on peut montrer que la luminosité du
phénomène, proportionnelle à la perte
d'énergie cinétique, varie de son côté
beaucoup plus vite, en fonction de la racine cubique du carré de
la masse (c'est-à-dire un peu moins vite que la masse).
Augmenter la masse suffisamment pour diminuer sensiblement le freinage
atmosphérique reviendrait donc à augmenter beaucoup plus
la luminosité théorique de l'objet, laquelle serait vite
incompatible avec les observations.
— L'altitude : si on augmente l'altitude, on augmente d'autant la
distance à laquelle le film a été pris (puisqu'on
connaît parfaitement la hauteur angulaire), et donc aussi la
vitesse d'après la vitesse angulaire observée sur le
film ; et en augmentant la vitesse, on augmente le frottement
atmosphérique... Bref on tourne un peu en rond, mais la
densité atmosphérique diminue tout de même plus
vite que le carré de la vitesse n'augmente, le bilan est donc
positif... Mais on ne peut tout de même pas aller trop loin, la
vitesse de l'objet étant limitée pour rester cohérente avec la vidéo.
— L'angle de descente : il est sans doute nécessaire de
l'augmenter un peu pour que l'objet ait conservé une bonne
partie de sa vitesse originelle, sans quoi on devrait considérer
qu'il était plus proche, donc à une altitude
inférieure, ce qui ramènerait au problème
précédent. Nous avons vu que les chercheurs espagnol du
SPMN estimaient un angle de descente très supérieur au
nôtre, mais difficilement conciliable avec certains
témoignages et incompatible avec le cap annoncé (il est
bien précisé que leurs calculs sont tout à fait
provisoires, et en outre ces chercheurs ne cachent pas qu'ils tiennent
pour l'instant à garder la trajectoire exacte secrète).
Il faut sûrement jouer un peu sur tout cela pour obtenir les
données les plus cohérentes possibles, et il
apparaît clairement qu'on ne peut pas faire ça « au
pif ».
Notons qu'il serait possible
a priori
d'observer le ralentissement sur la vidéo, mais compte tenu du
manque de définition de celle-ci et de la taille apparente du
météore c'est difficile. J'ai essayé, et il semble
bien y avoir un ralentissement assez net, mais difficile à
mesurer précisément... Disons qu'il doit être
compris entre 20 et 50%.
Pour aller plus loin dans nos supputations, il faut cette fois renoncer
à la se servir de la trajectoire hyperbolique suivie par un
objet dans le vide, et calculer pas à pas la trajectoire dans
l'atmosphère. On peut voir sur le schéma ci-dessous
comment procéder :
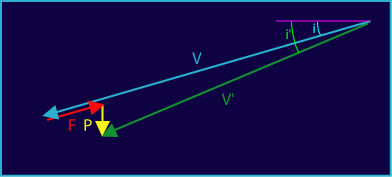
À partir de la vitesse et de l'angle de descente à un
instant donné (et connus dans le cas du temps de
référence), on calcule la vitesse et l'angle de descente
après un court intervalle de temps, en tenant compte du freinage
dû à l'atmosphère et de
l'accélération vers le bas due à la pesanteur. On
doit aussi tenir compte de la déviation de la verticale dû
à la courbure de la Terre, qu'il est facile de calculer en
fonction de la distance horizontale parcourue par l'objet pendant
l'intervalle de temps choisi.
En refaisant le calcul pas à pas, on a cette fois une bonne
idée de la trajectoire suivie par le météore
durant son parcours dans l'atmosphère terrestre.
On peut aussi de façon similaire « remonter le
temps », pour calculer la trajectoire avant le point de
référence... Et lorsque l'altitude est telle que
l'atmosphère n'a plus d'influence sensible, la vitesse du
météore doit être identique à celle que
donnait la trajectoire hyperbolique ne tenant pas compte du freinage
atmosphérique. Si ça n'est pas le cas, il faut modifier
au moins un des paramètres initiaux.
La feuille de calcul s'agrandit
Pour rester dans la continuité de ce texte, j'ai rajouté
pour faire ces calculs un tableau à la feuille de calcul
précédente... Vous pouvez télécharger la
nouvelle feuille de calcul (et cette fois il n'y en aura pas d'autre !)
Les données modifiables dans cette nouvelle partie sont la masse
du météoroïde, sa densité et l'intervalle de
temps considéré.
Cet intervalle doit être le plus petit possible pour que les
calculs soient précis, mais diminuer l'intervalle demande
d'augmenter le nombre de lignes de calculs pour suivre la trajectoire
sur une distance convenable. Un intervalle de 0,2 secondes semble un
compromis correct.
À partir de cela, le rayon du météoroïde est
calculé, ainsi qu'une constante regroupant les termes
invariables dans le calcul du freinage atmosphérique : tous sauf
le facteur de diminution de la densité atmosphérique et
la vitesse.
La « vitesse à atteindre », celle vers laquelle doit
tendre l'objet lorsqu'on « remonte le temps », est
assimilée à la vitesse théorique lors de
l'entrée dans l'atmosphère sur la trajectoire parabolique.
Les différentes colonnes indiquent à chaque pas :
— le temps par rapport à l'instant de référence,
incrémenté ligne après ligne de l'intervalle
choisi ;
— l'accélération, résultat du calcul que nous avons vu ;
— la perte de vitesse, décélération subie pendant l'intervalle de temps choisi ;
— la vitesse ;
— l'inclinaison de la trajectoire par rapport à l'horizontale ;
— l'altitude ;
— l'angle de grand cercle parcouru pendant l'intervalle de temps considéré ;
— la distance au sol par rapport au point de référence.
Au point de référence d'où partent les calculs
dans un sens et dans l'autre (temps 0), l'inclinaison est celle choisie
pour la trajectoire théorique, et la vitesse est la vitesse sur
la trajectoire théorique corrigée en fonction du
déplacement angulaire sur la vidéo.
Le but est donc de faire varier les paramètres de l'orbite vus
précédemment (cap, vitesse et altitude au point de
référence) de telle façon que la vitesse du
météore tende lorsqu'on remonte le temps (vers le bas du
tableau) vers la vitesse théorique. Quand on obtient cela,
toutes les données sont cohérentes (ce qui ne signifie
malheureusement pas qu'elles correspondent à la
réalité !)
Nouveaux compromis
J'ai porté sur la feuille de calcul les résultats qui
m'avaient semblé les plus vraisemblables, après moult
tâtonnements, mais vous pouvez essayer d'autres combinaisons.
Il semble nécessaire de choisir une altitude un peu
supérieure à celle estimée
précédemment (18 km), plutôt égale à
25 km (la densité atmosphérique est alors divisée
par 23 par rapport au sol). Cela modifie quelque peu les
coordonnées du point de référence, et j'ai
corrigé en conséquence les coordonnées de la lune
vue depuis ce point.
La distance augmente alors également, si bien que la masse de
l'objet a pu être sous-estimée. J'ai choisi de
considérer une masse de 20 tonnes, mais je rappelle que
l'influence de la masse est assez faible. Pour un objet de cette
taille, la perte de masse par ablation doit rester négligeable
jusqu'à cette altitude de 25 km.
La vitesse théorique doit de ce fait être aussi
augmentée ; on obtient un bon compromis pour une vitesse au point
de référence égale à 20,7 km/s, aboutissant
à une vitesse « à l'infini » de 17,7 km/s.
Enfin, le cap doit être diminué, égal à
46,5°. L'angle de descente s'en trouve porté à
18,9° contre les 13,5 que laissaient supposer une photographie du
météore... Ça s'accorde assez mal avec un des
témoignages de Bigorre, mais ça rend beaucoup plus
vraisemblable l'observation depuis Le Cannet signalée par un
lecteur sur le site de LCI. Et ça reste malgré tout
très inférieur à l'angle suggéré par
les chercheurs espagnols.
Tout cela a pour effet d'augmenter l'altitude à proximité
de la ville de León, portée à 45 km, et la
distance à laquelle se trouve l'objet lorsqu'il est
filmé, portée à 63 km.
On remarque aussi que l'objet se serait morcelé peu avant
d'atteindre la décélération maximale égale
à 3250 m/s
2 (plus de 300 g). Il aurait donc
« failli », si mes considérations sont valables (ce
qui est je le reconnais très incertain), atteindre le sol
entier, et offrir ainsi aux chercheurs une belle
météorite de plusieurs tonnes. Ils devront
malheureusement se contenter de quelques débris (sans doute tout
de même assez nombreux et assez gros pour certains).
Lieu d'impact
Essayons maintenant d'estimer le point supposé d'impact avec les
nouvelles données. La trajectoire hyperbolique nous donne un
point de chute à 75 km du point de référence, mais
cette distance est sûrement nettement plus courte en raison du
freinage atmosphérique.
Pour l'estimer vraiment, on pourrait prolonger les calculs pas à
pas jusqu'au point d'impact... Il faudrait pour cela rajouter un
certain nombre de lignes. Si vous avez une certaine habitude des
feuilles de calculs, vous pouvez le faire en insérant des lignes
vides puis en copiant sur chacune d'elle les huit cellules remplies
d'une ligne quelconque. Les calculs étant tous faits
relativement aux données présentes sur la ligne
inférieure, il n'y a rien à modifier.
Vous pourriez alors constater une incurvation progressive de la
trajectoire. Mais pour avoir une idée correcte de la
réalité, il faudrait aussi diminuer la masse de l'objet,
puisqu'après la fragmentation ce sont des morceaux nettement
plus petits que l'objet initial qu'il faut suivre, et de plus ils
perdent rapidement leur masse par ablation. Étant donné
que la masse de ces débris peut être très variable,
le résultat le sera aussi, et il y aura une « bande
d'impacts » plutôt qu'un point unique. En fait, ça
sera même plutôt une ellipse très allongée,
du fait que les divers débris sont légèrement
déviés lorsque la fragmentation explosive se produit.
N'essayons donc pas de trouver un chiffre précis, et estimons
que le milieu de cette bande doit se situer à une cinquantaine
de kilomètres du point de référence.
Pour calculer les coordonnées de ce point, j'ai encore
rajouté une ligne aux calculs situés à droite de
la feuille (ligne « Test »).
Pour cette distance de 50 km (que vous pouvez modifier), on trouve une
latitude égale à 43,0324°N et une longitude
égale à 4,4239°W : soit 43°01,9'N et
4°25,4'W. Un point situé près du « Pico de Tres
Mares », en pleine montagne à près de 2000 m
d'altitude.
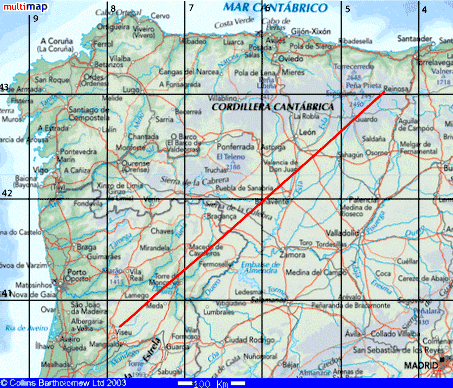
Voici donc la trajectoire révisée que nous obtenons :
Chasse aux météorites ?
Je rappelle que tout cela reste très hypothétique et
imprécis, d'une part parce que ça s'appuie toujours
essentiellement sur une analyse sans aucun contrôle sur place
d'une unique vidéo et quelques indications vagues et disparates,
et d'autre part parce que je ne suis pas du tout expert en
météorites.
Même si je ne me trompe pas trop dans toutes mes estimations
successives, il est extrêmement douteux que la trajectoire soit
précise au point d'impact à moins de deux ou trois
kilomètres près, et la distance à moins de dix
kilomètres... Ça serait déjà très
optimiste, et ça laisserait pas mal de surface à
explorer, surtout sur des montagnes enneigées !
Si ça vous tente quand même, un bon moyen de
détecter les météorites est le détecteur de
métaux, puisqu'elles contiennent souvent (et c'est le cas de celle-ci) une bonne proportion de fer.
Pour simplement les différencier d'un quelconque caillou bien
terrestre, et pour la même raison, un aimant suffit.
Il serait bon aussi d'interroger les habitants des villages
situés plus près sur la trajectoire (notamment Guardo)
pour essayer de préciser celle-ci. Ensuite, compte tenu du fait
qu'il pourrait y avoir un grand nombre de météorites
alignées le long de cette trajectoire, le plus simple serait de
suivre des lignes perpendiculaires à celle-ci, sur l'incertitude
de distance que vous choisirez... Je ne serais pas surpris que les
météorites découvertes à ce jour l'aient
été près des petits villages situés de part
et d'autre de la C 627 (San Salvador de Cantamuda, Los Llazos...)
Et je
ne serais pas surpris non plus qu'il y ait des météorites
un peu au-delà de la province de Palencia, qui pourraient
être trouvées à proximité des routes
CA 183
et CA 280.
Mais franchement, même sans tenir compte de la forte
probabilité que je me trompe assez fortement, l'entreprise
aurait peu de chances d'être fructueuse, et je rappelle que le
type de météorite concerné n'a que peu de valeur
marchande...
Orbite en 3D
Tant que j'y étais, j'ai rajouté dans la feuille de
calcul la section concernant le calcul d'orbite en 3D que je n'avais
pas eu le temps de faire à la dernière mise à
jour...
Je ne détaillerai pas les calculs, mais si ça vous
intéresse vous pourrez les comprendre en étudiant les
cellules concernées de la feuille de calcul. Par rapport au cas
déjà vu d'une orbite dans le plan de l'écliptique,
il faut commencer par étudier le « triangle des
vitesses » projeté sur l'écliptique, puis en
déduire la vitesse et la direction de l'objet sur son orbite
réelle.
Le reste n'a pas changé, si ce n'est qu'il faut aussi calculer
l'inclinaison orbitale. Puisque l'orbite coupe l'écliptique
précisément à la position où se trouve la
Terre (ça n'est pas tout-à fait vrai dans le cas d'une
orbite très peu inclinée), l'inclinaison sera celle de la
direction de l'astéroïde projetée sur un plan
perpendiculaire au rayon vecteur de l'orbite.
Avant de calculer l'orbite, il faut convertir les coordonnées
locales du radiant (le point d'origine apparente du
météore) en coordonnées écliptiques. Et
puisque j'ai encore eu la flemme d'automatiser ce changement de
coordonnées, il faut encore passer par un logiciel d'astronomie.
À partir du point correspondant au radiant calculé du
météore, vous devez chercher la distance angulaire de
l'écliptique (positive si le radiant est au-dessus de
l'écliptique), puis à partir de ce point projeté
sur l'écliptique chercher l'angle par rapport au soleil (positif
si ce point se trouve à gauche du soleil)... Tous les bons
logiciels d'astronomie permettent de calculer les distances angulaires
entre deux points de la voûte céleste.
Avec les paramètres que j'ai retenus, on trouve
un radiant à un azimut de 227,1° et une hauteur de
12,1°. On obtient alors pour les coordonnées
écliptiques une hauteur de 0,2°, et un angle par rapport au
soleil de 15°.
On voit donc curieusement que le radiant se trouve très
près de l'écliptique (le calcul en 3D n'est pas vraiment
nécessaire dans ce cas !), et je ne l'ai vraiment pas fait
exprès... Ça tend à confirmer mon intuition de
départ sans laquelle je ne me serais jamais lancé dans
cette affaire !
Les autres paramètres trouvés sont :
— inclinaison orbitale = 0,1° ;
— angle du grand axe par rapport au point de rencontre de la Terre (le noeud descendant de l'orbite) = 116,6° ;
— grand-axe = 884,8 gigamètres ;
— durée de révolution = 1857 jours (5,08 ans) ;
— excentricité = 0,74 ;
— périhélie = 114,4 gigamètres ;
— aphélie = 770,4 gigamètres.
Une autre curieuse coïncidence est que l'aphélie correspond
pratiquement à la distance de Jupiter au Soleil. Bien que
Jupiter soit la principale cause des déviations
d'astéroïdes, les orbites très elliptiques ont
tendance à se circulariser en raison de l'influence des autres
planètes, et il n'y a donc pas vraiment de raison d'obtenir un
tel résultat. Combiné à la très faible
inclinaison de l'orbite, ça pourrait donner à penser que
l'astéroïde responsable aurait été
dévié par Jupiter assez récemment, mais il y a de
grande chances que ça relève surtout de la
coïncidence.
Je rappelle d'ailleurs que tout cela reste très incertain et
imprécis, bien plus encore que la trajectoire dans
l'atmosphère. Mais il sera toujours intéressant de
comparer nos estimations très hypothétiques et faites
à partir de presque rien avec les résultats des
scientifiques espagnols qui étudient les données
précises.
Additif (17/03/2004)
Note : un passage concernant la découverte d'un nouveau morceau
de cette météorite a été
momentanément supprimé à la demande du
découvreur... Nous avons accédé à sa
demande en attendant plus d'informations, mais nous ne manquerons pas
de donner en temps utile toutes les explications sur ce revirement.
Quand l'astronomie rencontre l'ufologie
Je pense avoir montré qu'on peut être ufologue et ne
pas ignorer les notions d'astronomie, contrairement à ce que
semblent croire beaucoup d'astronomies...
Citons à ce propos, justement, le site du SPMN au sujet de ce météore en Espagne :
Il y a encore quelques années
cet événement impressionnant aurait pu facilement et
malheureusement être relégué à des
observations inexpliquées d'ovnis. Toutefois, ces
phénomènes ont cessé d'être NON
IDENTIFIÉS aujourd'hui parce qu'actuellement une bonne partie du
public dispose de caméscopes avec lesquels filmer ces
événements impressionnants. En outre, notre Réseau
de recherche sur les bolides et météorites, grâce
au travail d'une équipe de jeunes scientifiques espagnols, a
entrepris d'utiliser de nouvelles techniques d'images et de traitement
informatique, pour donner une explication rationnelle de ces
phénomènes sur la base d'arguments solides et
convaincants.
Bref, à les croire, s'ils n'avaient pas été
là il n'y a aucun doute que ce phénomène n'aurait
attiré l'attention que de stupides ufologues bien
évidemment incapables de faire la différence entre un
météore et un crash de soucoupe volante !
Je suis un peu amer envers ce groupe de recherche espagnol non
seulement pour cette phrase qui est assez révélatrice du
manque de considération qu'ont la plupart des astronomes pour
l'ufologie (pas tous heureusement), mais aussi parce que les courriers
que m'a adressé son directeur et webmestre, le
Dr Trigo-Rodrigez, n'ont pas été
particulièrement
courtois.
Dans la première version de mon article sur le
météore d'Espagne, j'avais utilisé une photo et
une carte extraite de leur site, en précisant bien comme
c'était demandé dans les légendes qu'elles
provenaient du
Red de investigación sobre bólidos y meteoritos
et en plaçant des liens pointant sur leur site (ça
n'était pas demandé mais ça me paraissait normal),
que je citais comme la source d'informations la plus
intéressante concernant ce phénomène. J'avais
aussi superposé pour comparaison la trajectoire que j'obtenais
de façon tout à fait indépendante à leur
« trajectoire préliminaire »...
Le Dr Trigo-Rodrigez, que j'avais informé de ce texte,
m'avertissait en réponse que « pour publier leur
données, photographies et trajectoires je devais leur accorder
l'entier crédit, en incluant les noms et affiliations de leur
groupe à chaque fois que je le mentionnais » (il me
semblait bien l'avoir fait !) et que je ne devais pas ajouter ma
trajectoire sur leur image originale, et que si je persistais je
m'exposerais à des poursuites judiciaires (encore... On va finir
par penser que je les attire !)
J'avais donc immédiatement remplacé la carte de leur
trajectoire superposée à la mienne par une carte de ma
trajectoire sur laquelle j'avais retracé la leur (qu'ils avaient
du reste immédiatement modifiée pour l'écarter un
peu plus de la trajectoire réelle, dont la mienne s'approchait
déjà dangereusement !), et rajouté tous les
renseignements possibles sur leur groupe avec l'équipe ayant
participé au complet... S'il n'y avait que ça pour leur
faire plaisir...
Après cela, le second courrier était tout à fait cordial.
Mais lorsque j'ai informé le Dr Trigo-Rodrigez de mon additif du
25 janvier, il n'était de nouveau pas content et me demandait de
corriger sans tarder mon texte parce qu'il estimait que je donnais des
informations qui n'étaient « pas très polies sur
leur travail », alors que les données qu'ils publiaient
n'étaient que préliminaires et ne visaient qu'à
essayer d'intéresser le public à l'astronomie... Tout
ça apparemment parce que j'avais écrit : « je reste
par ailleurs persuadé que le groupe du SPMN devra aussi
réviser à la baisse l'angle de descente du
météore ». Il me reprochait aussi d'avoir
mentionné sans son accord une précision extraite de son
courrier sur ce qu'il entendait par « vitesse d'entrée dans
l'atmosphère ». Un peu excédé, je supprimai
donc cette précision en indiquant qu'il ne semblait pas
désireux de lever le doute, et l'informai que pour le reste ils
étaient libres de fournir au public une trajectoire
faussée mais que j'étais libre de le dire, et que j'avais
été suffisamment « poli avec leur travail » en
écrivant notamment dans ce même additif, dans un
paragraphe intitulé « la suite appartient aux
spécialistes » :
Les
chercheurs espagnols ont de leur côté bon espoir d'arriver
à une précision suffisante pour déduire les
caractéristiques de l'orbite, ce qui serait je crois une
première pour un météore observé de jour...
On peut leur faire confiance en tout cas pour tirer le maximum des
documents dont ils disposent !
Et je n'en continue pas moins à souhaiter au SPMN une totale
réussite dans sa tentative de reconstituer l'orbite de l'objet
avant sa rencontre avec la Terre.
Au sujet du rejet qu'ont beaucoup d'astronomes sur la recherche ufologique, je voudrais aussi citer l'exemple du salon
Astronomia 2004,
qui doit se tenir à Liévin du 14 au 16 mai prochain. Les
organisateurs dynamiques de cette manifestation rêvaient d'une
grande exposition et de conférences ayant trait aussi bien
à l'astronomie qu'à l'ufologie, sous le thème
fédérateur de l'exobiologie. Ils avaient pris contact
avec des ufologues sérieux en se rendant aux Repas ufologiques parisiens,
un site avait été créé pour annoncer ce
« plus grand salon astro-ufo de France » et son programme
préliminaire, ça s'annonçait comme une
réussite... Mais sous la pression très forte des
instances scientifiques et des autorités locales, les
responsables ont été contraints, pour ne pas dire
franchement sommés sous peine de représailles
professionnelles, de supprimer la branche ufologie !
Maintenant, le site a disparu, et ce salon n'est plus guère
annoncé que dans l'agenda du CNRS, avec un programme
exclusivement astronomique et bien conformiste...
Le CNRS qui considère sûrement, après avoir reçu le
« rapport Louange »,
que seul le CNES et son Service d'expertise des
phénomènes rares atmosphériques peut
étudier les ovnis avec le sérieux qui convient pour avoir
le droit de côtoyer les astronomes...
Et pendant que le directeur de ce SEPRA était payé pour
déclarer à la presse les pires énormités
sur ce météore en Espagne, et arrondissait ses fins de
mois
en s'appropriant les économies d'un RMIste ayant osé
dénigrer son travail d'expert en rentrées
atmosphériques, le RMIste ufologue en question, sans autre but
que d'initier un peu le public aux méthodes utilisables pour
retracer des trajectoires de météores, bref en faisant
bénévolement le travail d'information dévolu au
SEPRA et que ce dernier n'avait jamais fait en quinze ans d'existence,
aidait à la découverte de nouveaux fragments de cette météorite... C'est beau, le monde
scientifique et ses grandes institutions au sérieux
incontestable...
Robert Alessandri




Ce texte a été lu
fois depuis le 17/03/2004