Un météore exceptionnel en Espagne
le 4 janvier 2004
(22/01/2004)

Ce dimanche-là à 17 h 47 locales (même heure en France), des milliers d'Espagnols dans pratiquement tout le pays ont vu une boule de feu éclatante traverser le ciel peu avant le coucher du soleil.

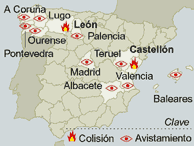
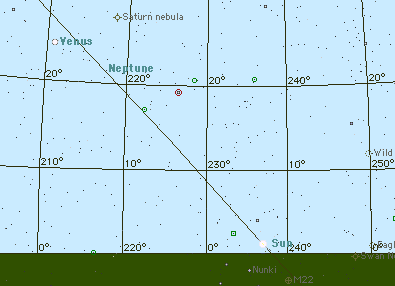
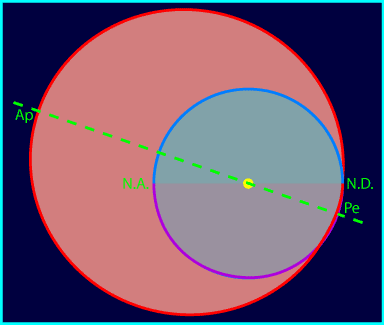
Voici pour vous repérer une carte de l'Espagne, avec la limite jour/nuit à l'heure dite (nous verrons que ça aura son importance). Vous pouvez l'ouvrir dans une fenêtre séparée en cliquant dessus.

Errements initiaux

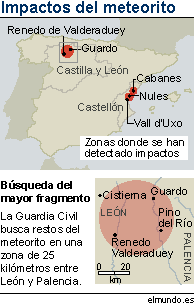
Le lendemain, les informations se sont multipliées dans la presse et sur Internet. El Mundo publiait notamment un long article indiquant que le météore aurait traversé l'Espagne du nord-ouest à l'est, et que plusieurs débris seraient retombés, provoquant des départs de feu... Ces cartes présentaient les zones de ces « impacts », activement fouillées par la Garde Civile.


On voit que la trajectoire supposée du météore reflétait assez bien l'alignement apparent des témoignages...

Le phénomène a été vu à St-Jacques de Compostelle, au nord-ouest, notamment par les spectateurs d'un match de football. Parmi eux se trouvait le directeur de l'observatoire de la ville, José Angel Docobo, qui avait vu le météore à environ 30° au-dessus de l'horizon en direction de l'est. L'astronome estimait par ailleurs sa masse entre 50 et 100 tonnes, ce qui était sans doute un peu exagéré. On peut trouver ses premières déclarations sur le site d'El Correo Gallego.

C'est dans les régions de León et de Palencia (nord-nord-ouest de Madrid) que le phénomène a été le plus spectaculaire, et accompagné d'un fort bruit d'explosion. C'est là que le principal départ d'incendie a été signalé, et que la Garde civile a cru trouver des traces d'un impact.

Le phénomène a aussi été vu dans l'est de l'Espagne, et jusqu'aux îles Baléares...

Cet alignement approximatif des premières observations signalées avait inspiré les premières annonces de trajectoire, mais on ne citait pratiquement aucun témoin ayant mentionné la direction de l'observation ou le cap suivi par l'objet ! Cet alignement était en fait fortuit, puisqu'on trouvait aussi de nombreux témoignages au Portugal, aussi bien dans le nord que dans le centre du pays (mais très peu semble-t-il dans le sud)... La barrière linguistique a sûrement joué un rôle dans les incohérences des premières informations.

Le directeur de l'observatoire de Lisbonne, Rui Agostinho, estimait que « les Espagnols faisaient une estimation très exagérée », et que l'objet devait peser quelques centaines de kilogrammes... C'était sans doute ici sous-estimé, peut-être parce que le phénomène a été moins lumineux au Portugal qu'en Espagne !

Le fait qu'il faisait nuit dans le nord-est de l'Espagne et aux Baléares (et aussi en France, nous y reviendrons) rendait en outre le phénomène visible de beaucoup plus loin dans ces régions, parachevant cette répartition trompeuse.

Dès le lendemain des faits, une équipe du Conseil supérieur d'enquêtes scientifiques (CSIC, Consejo Superior de Investigaciones Científicas) a été dépêchée afin de déterminer si le météore avait été responsable de l'incendie ayant brûlé trois hectares de forêt à Minglanilla, et si l'on trouvait des traces d'impact comme la Garde civile l'avait suspecté. Mais le six, ce groupe concluait qu'il n'y avait dans cette région aucun indice d'impact météoritique, et que l'incendie n'avait aucun lien avec le phénomène.

Il faut dire que les incendies causés par des météorites sont très exceptionnels. La grande majorité des météorites arrivent au sol froides, quelquefois même glacées. En effet, seule la couche superficielle est chauffée par le frottement de l'air, et la chaleur n'a pas le temps de gagner les régions centrales. Quand elles atteignent le sol, les météorites ont généralement perdu la plus grande partie de leur vitesse et ne sont donc plus que très peu échauffées, et elles refroidissent presque instantanément.

Seules des météorites de grande taille peuvent percuter le sol à grande vitesse et être encore brûlantes en surface, et dégager en outre beaucoup d'énergie lors de l'impact. Elles peuvent alors provoquer un incendie, mais c'est rarissime. Le seul cas attesté dans l'histoire récente est celui d'une météorite, que l'on a retrouvée, ayant déclenché un incendie le 17 avril 1934 près de Séville, en Espagne justement. Le château de Milan (Italie) aurait de son côté été dévasté par un incendie en 1525 (ça ne date pas d'hier !) par le fait d'une météorite malencontreusement tombée dans la salle des munitions !

Bref, compte tenu de la dimension estimée de l'objet, l'incendie allégué n'était pas vraiment impossible, mais restait très improbable. On sait maintenant qu'aucun incendie n'a été provoqué par le météore, bien que des météorites aient atteint le sol (précisons que le terme de météore désigne le phénomène lumineux, celui de météorite les éventuels fragments trouvés au sol).

Ajoutant encore à la confusion, la chaîne télévisée Antenna 3 diffusait le 5 une vidéo prétendue d'un autre météore qui aurait été filmé le 3 à 18 h 07, la veille de celui que tout le monde avait vu... Voici deux parties d'images extraites de ce film :


Ça n'a manifestement rien à voir avec un météore, et il s'agit certainement de la simple traînée d'un avion éclairée par le soleil couchant. La nette division en deux de cette traînée est caractéristique... Cette volonté de présenter à tout prix des images, fussent-elles sans rapport avec l'événement, rappelle un peu les photos des lumières clignotantes d'avions que certains journaux peu scrupuleux ou mal informés (VSD et Paris-Match) ont présentées à plusieurs reprises comme des photos de la rentrée de satellite du 5 novembre 1990, avec la caution de l'expert du CNES en rentrées atmosphériques !

L'affaire se précise

Mais les premières déductions correctes allaient venir d'une autre vidéo, celle-là authentique, tournée dans la ville de León, dont on a vu qu'elle était de toute façon proche du survol du phénomène... En voici une image. Vous pouvez télécharger la vidéo en cliquant dessus.


Cette vidéo est intéressante parce qu'elle montre dans la direction visée un mur éclairé, apparemment presque perpendiculairement (on ne voit pas d'ombre projetée par les balcons), par le soleil. Le soleil se trouvant alors au sud-ouest (précisément azimut 237°), on pouvait en déduire que la prise de vue était faite vers l'est... Et cela signifiait que le météore se déplaçait sensiblement du sud-ouest au nord-est, contrairement à tout ce qui avait été dit !

Et le 9 janvier, Victor Ruiz, un passionné de météores habitué de la liste de diffusion Meteorobs, relevait un détail encore plus important : on voit juste à gauche de la fenêtre de l'avant-dernier étage du bâtiment éclairé par le soleil un petit point lumineux... Ce point garde une position fixe par rapport au bâtiment alors que le caméscope bouge beaucoup, il ne peut donc pas s'agir d'un reflet... Et Ruiz a compris que ce point lumineux n'était autre que la Lune... Un coup de chance puisqu'on connaît parfaitement sa position à ce moment : 23° de hauteur et azimut de 79°. Et puisque le météore passe juste à côté, on peut affirmer que la trajectoire était bien sud-ouest/nord-est... Et ça donne aussi une idée de la luminosité de l'objet, surtout lorsqu'il émet un « flash » impressionnant ! C'est bien un météore très exceptionnel qui a survolé l'Espagne.

D'autre part, la forte détonation entendue après le passage du bolide dans cette région trahit un passage à moins de 50 km d'altitude, la densité atmosphérique étant trop faible pour transmettre l'onde de choc au-delà. Le phénomène étant sans doute passé à environ 60° de hauteur angulaire, on peut en déduire que la projection au sol de la trajectoire passait à moins de 30 km de cette ville.

Cette détonation a sans doute aussi inspiré les rumeurs d'impact dans ces régions : en effet, le son parvient plusieurs minutes après la disparition de l'objet à l'horizon, donnant l'impression qu'il s'est écrasé au sol. Il est vrai que les météores peuvent aussi faire entendre du bruit de façon presque instantanée, les rayonnements radio qu'ils émettent provoquant parfois des vibrations en touchant certains terrains particuliers ; mais il s'agit alors de bruits légers, grésillements ou sifflements, n'évoquant pas du tout une explosion.

Notons qu'on a diffusé une autre photo censée représenter le météore passant près de la lune, mais prise cette fois de Madrid par Enrique Gómez à 18 h 04 (détail) :


Mais là encore il s'agit manifestement d'autre chose (un quart d'heure après le passage du bolide si l'heure indiquée est exacte), sans doute encore la traînée d'un avion reflétant le soleil ! Il est tout à fait impossible que le même objet ait été vu en direction de l'est très lumineux à León, et à la même hauteur angulaire, dans la même direction mais beaucoup moins lumineux à Madrid qui se trouve à l'est de León !

Il y a enfin une autre photo prise près de León, qui recoupe tout à fait la vidéo :


Photo de Salvador Diez ; crédit : Red de Investigacion sobre Bólidos y Meteoritos (Spanish Fireball Network).

Enfin, la chaîne Antenna 3 a mentionné à deux reprises la découverte de météorites... La première aurait été trouvée près de Zamora, au sud de León, ce qui pourrait correspondre assez bien à la trajectoiredu météore... Toutefois, l'examen de l'objet semble démentir son origine météoritique. Une autre, découverte plus récemment, a traversé une serre à Villalobar, à une vingtaine de kilomètres au sud de León. Ça s'accorderait aussi très bien avec la vidéo et un passage à proximité de cette ville, mais là encore l'origine météoritique a été démentie...

Observations en France ?

Nous en sommes là pour l'instant des informations provenant d'Espagne (du moins j'en étais-là quand j'ai commencé à rédiger cet article... Mais j'y ai consacré plus de temps que je ne l'avais prévu, si bien que les informations se sont accumulées depuis... Nous ferons le point à la fin)...

Mais puisque le phénomène se déplaçait vers le sud-ouest de la France, a-t-on des témoignages de notre côté des Pyrénées ? Il semble que oui... Des ufologues ont parlé de témoignages dans la région de Dax, mais sans donner de détails... J'attends toujours de connaître des témoignages.

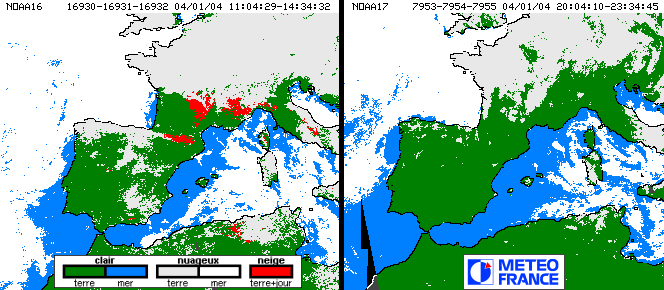
Notons que ce jour-là, il faisait beau sur pratiquement toute l'Espagne et le sud de la France, comme le montrent ces extraits de cartes du satellite NOAA (à gauche en début d'après-midi, à droite tard le soir) :


La météo était donc très favorable à l'observation du météore, aussi bien en France qu'en Espagne. D'autre part, en France, le soleil venait de se coucher, rendant un phénomène lumineux beaucoup plus visible. Les témoignages semblent pourtant très rares dans notre pays, ce qui indique que le météore a terminé sa course avant de l'atteindre... Dommage !

Un témoignage étonnant a été donné sur le le site de la chaîne d'information LCI, à la suite d'un article relatif à ce météore :

le 05/01/2004 à 17h33
J'ai vue aussi la méteorite tomber dimanche soir,lorsque je rentre chez moi,car j'avais passe la journée a faire du skie dans les Alpes du Sud a Auron,j'ai bien vue cette boule de feu dans le ciel,j'ai dis a ma soeur regarde dans le ciel l'étoile filante,mes vue la dure de vie,j'ai dis ces pas une étoile,cs un petit méteor car lorsque l'on la bien regarde on voyer bien une longue trainer et au devant une boule de feu avec 2 couleur jaune devant et vert en traine,voila(ces pas E.T qui es passer dommage :-( )bye bye,merci de passe mon message
Stevens, Le cannet-06(france)

J'ai laissé un message pour essayer d'en savoir plus, mais LCI ne l'a pas passé... Les journalistes sont là pour vendre leurs journaux, pas pour aider la recherche...

Le Cannet se trouve à 1025 km de León ! Ça n'est pourtant pas impossible, et finalement les Baléares où des témoignages ont été attestés ne sont pas beaucoup plus loin. Certes, il est impossible de voir à 1000 km un objet qui survole León à moins de 50 km du sol... Mais un météore devient lumineux bien avant de pénétrer aussi profondément dans l'atmosphère, à partir de 150 km ou plus... C'est probablement l'altitude qu'avait le météore lorsqu'il survolait le Portugal. Il pouvait alors être vu jusqu'à une distance de 1390 km pour peu qu'on bénéficie d'un horizon dégagé, plus que la distance entre Le Cannet et Porto (1140 km). Bien sûr, la densité de l'atmosphère à cette altitude est beaucoup moins importante qu'à 50 km, et donc l'échauffement est moindre, mais compte tenu de la taille de l'objet et du fait qu'il faisait nuit au Cannet (et aux Baléares) il devait atteindre à cette distance une luminosité proche de celle de Vénus.

Une photo aurait-elle été prise de France ? Le 4 janvier à 22 h 06, quelques heures seulement après l'observation, Le site Yahoo actualités publiait dans la rubrique « insolite » le texte suivant (qui n'est plus dans les archives) :

Boule de feu dans le ciel espagnol

MADRID (AFP) - Des centaines de témoignages de personnes ayant vu une boule non-identifiée dans le ciel espagnol dimanche soir sont parvenus à la garde civile qui a confirmé qu'un objet non identifié, sans doute, une météorite, était tombé dans la région de León dimanche en début de soirée.

Une boule de feu a été aperçue à la fois par des gens près de Saint-Jacques de Compostelle (Galice) aussi bien que par des témoins près de Saragosse (Aragon) ou dans la banlieue nord de Madrid.

D'autres témoins ont affirmé avoir entendu une sorte d'explosion près de León où est tombé l'objet. La garde civile a précisé qu'elle avait pris contact avec les aéroports de la région pour s'assurer qu'aucun avion n'était porté manquant.

Ça n'est rien d'autre que la première dépêche AFP, mais le texte était accompagné, sans aucun commentaire, de la photo suivante :


Ça ressemble bien à un gros météore, mais d'où cette photo aurait pu être prise, de nuit et montrant le phénomène se déplaçant de droite à gauche ? S'il s'agit de la photo du météore d'Espagne et si elle n'a pas été inversée, elle n'a pu être prise que de France, très au nord et même au nord-ouest... Ça serait d'ailleurs cohérent avec l'observation très bas sur l'horizon et la petite taille de l'image, indiquant que le phénomène a été photographié de très loin. Le seul problème, c'est que comme nous l'avons vu le ciel était plutôt nuageux dans toute la moitié nord de notre pays.

En fait, il s'agit d'une photo d'archives que l'on ressort régulièrement pour illustrer des informations concernant des météores... Jennifer Fillaux, après avoir lu la première version du présent texte, m'a informé que cette photo était extraite d'une vidéo tournée si elle se souvient bien en Italie en 1999... Fausse alerte donc.

On a besoin de témoins

On a donc beaucoup d'observations, mais plus d'une semaine après le phénomène (presque trois maintenant, je vous ai dit que ça m'a pris plus de temps que prévu !), personne n'a encore annoncé la trajectoire précise du phénomène (une « trajectoire provisoire » a depuis été annoncée, nous en reparlerons)... Il est vrai que contrairement aux satellites, les météores ne suivent pas des orbites précises que l'on peut trouver sur Internet ! La trajectoire ne peut être déduite que des observations, et il faut encore trouver des témoins qui donnent des informations exploitables : direction d'observation, hauteur angulaire, cap estimé, vitesse angulaire...

De tels témoignages sont d'autant plus indispensables que dans ce cas particulier, il est fort probable que des débris, des météorites donc, aient atteint le sol... Et récupérer des météorites peu après leur chute, avant qu'elles aient pu être contaminées par la Terre, peut être très important pour la recherche scientifique. Même si nous allons voir qu'on peut grossièrement évaluer la trajectoire sans beaucoup d'informations, l'estimation sera d'autant plus précise qu'il y aura de témoignages à confronter.

Même les observations faites en France pourraient s'avérer particulièrement utiles, c'est pourquoi je lance un appel aux témoins, et je serais reconnaissant aux autres gestionnaires de sites de le faire suivre. Je transmettrai les témoignages que j'aurai reçus aux spécialistes qui étudient cette affaire en Espagne, afin de les aider dans leurs recherches (puisqu'il semble exclu que l'on puisse trouver quelque chose en France).

Estimations de trajectoire

Ceci dit, je me risquerai tout de même à quelques hypothèses afin de déterminer la trajectoire... Sans prétendre faire mieux que les Espagnols qui disposent de quantités de témoignages pour la calculer, et d'astronomes professionnels pour les étudier. Voyez cela comme un exercice pour nous familiariser avec les calculs d'orbites... Et le « nous » n'est pas une formule de politesse, puisqu'étudier cet événement m'aura appris pas mal de choses sur les trajectoires de météores ; je m'étais surtout limité à celles des satellites, et c'était bien plus simple !

Si vous faites une allergie aux mathématiques, ou si vous avez tout oublié des notions élémentaires d'algèbre et de trigonométrie, allez directement à la fin de l'article consulter les dernières informations et les conclusions... Tout ce qui va suivre est juste destiné à faire comprendre que la mécanique orbitale, ça n'est pas aussi compliqué qu'on peut le penser, mais il faut tout de même être un peu matheux !

Pour qu'un astéroïde puisse heurter la Terre, il faut bien sûr que son orbite évolue entre une distance minimale au Soleil (périhélie) inférieure au rayon de l'orbite terrestre, et une distance maximale (aphélie) supérieure. Mais cela ne suffit pas, il faut aussi que son orbite coupe celle de la Terre, ce qui exige une des deux conditions suivantes :

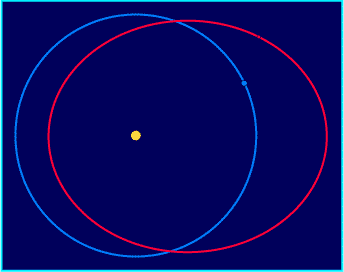
— soit l'orbite se trouve dans le même plan que celle de la Terre, l'écliptique, auquel cas les orbites vont se couper en deux points :


— soit le plan de l'orbite est différent de celui de la Terre, et dans ce cas il faut que le grand axe de l'orbite de l'objet soit dirigé de façon très particulière, lui faisant couper l'orbite terrestre en un seul point :


A priori, si les caractéristiques des orbites sont aléatoires, les deux conditions ont à peu près autant de chances l'une que l'autre d'être vérifiées (il n'y a qu'un point d'intersection dans le second cas, mais quatre angles convenables pour le grand axe, contre deux pour l'inclinaison de l'orbite dans le premier — 0 ou 180°). C'est le cas avec les comètes non périodiques provenant des confins du système solaire. Par contre, la grande majorité des astéroïdes et un bon nombre de comètes périodiques tournent dans un plan très proche de celui de la Terre, et dans le même sens que celle-ci : avec les astéroïdes, il y aura donc beaucoup plus de chances que la première condition soit vérifiée, plutôt que la seconde... Les comètes périodiques peuvent être exclues d'emblée puisque celles qui coupent l'orbite terrestre sont responsables des « essaims » d'étoiles filantes en raison des poussières et débris qu'elles laissent dans leur sillage, et aucun ne peut être lié à ce météore (l'essaim des « quadrantides » était très actif à cette époque, mais la direction suivie n'était pas compatible).

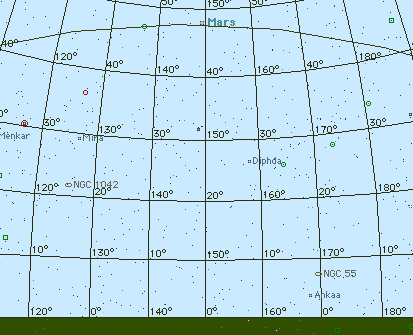
Voyons maintenant comment se situait la Terre dans l'espace au moment de l'événement (donnée par le logiciel d'astronomie MPJ Equinox, que je vous recommande au passage et qui va beaucoup nous servir) :


On voit que l'Espagne, et précisément la région de León, se trouvait pratiquement sur la limite entre jour et nuit (ce qui signifie que c'était le coucher du soleil). Or, il se trouve que sur la vidéo de León, le météore a l'air de provenir sensiblement de la direction du Soleil, et sur une trajectoire peu inclinée par rapport à la surface terrestre. Cela serait compatible avec un astéroïde dont l'orbite couperait celle de la Terre en s'éloignant du Soleil, plutôt qu'avec un objet de nature cométaire qui pourrait provenir de n'importe quelle direction... En outre, les morceaux de comète plongent rarement dans la basse atmosphère, leur matière très fragile (essentiellement de la glace) se vaporisant très vite. On peut donc privilégier l'hypothèse d'un petit astéroïde plutôt qu'un morceau de comète (précisons que les comètes que l'on voit parfois ne se consument pas dans l'atmosphère : elles sont très loin de la Terre et ce que l'on voit c'est une queue de gaz et de poussières libérés en raison de l'échauffement par le Soleil, et repoussés par ses rayons lumineux)... Il n'empêche qu'une comète ou un débris cométaire de toute taille peut très bien heurter la Terre, et ça donne à peu près la même chose qu'un astéroïde : un météore, sinon qu'on ne trouve jamais de débris au sol, de météorites.

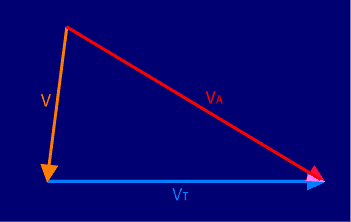
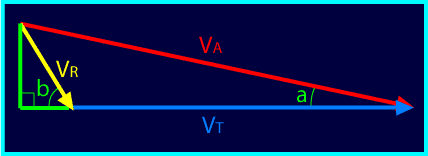
On peut voir sur le schéma ci-dessous comment calculer la vitesse apparente d'un astéroïde d'après sa vitesse sur son orbite :


La vitesse de la Terre est V_T, celle de l'astéroïde est V_A, et la vitesse apparente par rapport à la Terre sera V. Notons que dans le cas d'essaims d'étoiles filantes, le radiant, direction du ciel d'où semblent provenir les météores (une étoile filante est un petit météore ; les gros, comme celui qui nous occupe, sont appelés « bolides » ou « boules de feu »), correspond à la direction opposée à cette vitesse relative... Elle est très différente de la direction suivie par ces débris de comètes dans l'espace (V_A). Pour mieux comprendre, imaginez que vous heurtez une automobile venant de votre gauche à un carrefour, si vous allez à la même vitesse qu'elle vous ne la verrez pas arriver à angle droit, mais à 45°.

La Terre se déplace sur son orbite à la vitesse de 30 km/s, et l'astéroïde se déplace de son côté sur une orbite ellipsoïdale, à une vitesse qui dépend de la forme de cette orbite. Précisément, la vitesse à une distance donnée du Soleil dépend du grand-axe de l'orbite, selon une formule simple :

(V/V_C)² = 2-2D/G_A

V_C est la vitesse de satellisation circulaire à cette distance, c'est donc celle de la Terre, 30 km/s, et D est la distance du Soleil, 150 gigamètres (je sais, c'est sans doute la première fois que vous voyez employer une telle unité, mais n'est-ce pas plus simple que « millions de kilomètres », puisque c'est la même chose ? je ne comprends pas que l'on parle couramment de gigawatts ou de gigaoctets mais pas de gigamètres ! Donc, habituez-vous).

Il y a deux cas extrêmes :

— si l'orbite est une ellipse très aplatie dont le périhélie est très proche du Soleil, le grand-axe se rapprochera de D, et la vitesse sera nulle (l'astéroïde « tombe » alors sur le Soleil) ;

— si au contraire l'orbite est une parabole, c'est-à-dire une ellipse dont le grand-axe est infini, la vitesse est égale à la vitesse de la Terre multipliée par √2, soit 42 km/s. Elle n'est jamais plus importante : cela supposerait un astéroïde provenant de l'infini à une vitesse non nulle ; ça n'est pas strictement impossible, il y a bien des événements violents dans l'Univers capables de projeter un objet vers le système solaire à une vitesse importante, mais ça n'a jamais été observé.

La direction suivie détermine la forme de l'orbite : il n'y a qu'une ellipse ayant un grand-axe donné, dont le Soleil occupe un foyer, qui touche tangentiellement le point d'application de la vitesse.

En règle générale, les astéroïdes proviennent de la ceinture d'astéroïdes entre Mars et Jupiter, dont ils ont été délogés par l'influence d'une de ces planètes. Leur aphélie se trouve donc souvent dans ces parages-là, à deux à trois fois la distance de la Terre (en fait, il est souvent plus proche du Soleil que cela, les perturbations lors du passage à proximité d'une planète ayant tendance à circulariser l'orbite). Et puisque le fait qu'ils atteignent les parages de la Terre résulte d'une perturbation, ceux qui auront été le moins « perturbés », les plus nombreux, n'auront pas un périhélie très inférieur à celui de la Terre... On peut donc admettre comme moyenne un grand axe égal à 3,5 unités astronomiques (on appelle ainsi le rayon de l'orbite terrestre, égal à 149,6 gigamètres ; c'est une unité pratique pour exprimer les distances à l'échelle du système solaire), ce qui implique une vitesse de 36 km/s au niveau de la Terre.

Si la trajectoire apparente de l'objet vient précisément de la direction du Soleil, le triangle représentant les vitesses est rectangle, et la vitesse apparente de l'objet lorsqu'il s'approche de la Terre s'exprime très simplement :

√(36²-30²) = 20 km/s.

Admettons donc cette valeur comme hypothèse de base.

Puisqu'un astéroïde a toutes les chances d'avoir son orbite pratiquement dans le même plan que celle de la Terre, la trajectoire d'arrivée sera nécessairement parallèle à ce plan.

On sait que la ville de León n'est pas très loin du point de chute supposé, et d'autre part c'est de là qu'a été prise la vidéo qui nous permettra des calculs précis... León se trouve à 42°35' de latitude nord, et à 5°34' de longitude ouest... Pour simplifier les calculs, nous allons plutôt estimer un lieu survolé par le météore, et plus exactement le lieu où il passait lorsqu'il était filmé depuis León...

Nous nous limiterons pour l'instant à une estimation grossière, que nous corrigerons en fonction des résultats des calculs. Nous savons d'après la position de la Lune que le météore était filmé à une hauteur sur l'horizon d'environ 23° et à un azimut d'environ 74°. Nous savons aussi que son altitude était suffisamment basse lors de son passage près de León pour provoquer une forte détonation. Admettons qu'il se trouvait à une altitude de 20 km au moment où il était filmé... Ça nous permet d'estimer la distance au sol :

20 km/tangente 23 = 47 km.

Et dans un azimut de 74° en partant de la position de León, on peut calculer simplement, en négligeant la courbure de la Terre, les coordonnées de notre « point de référence» provisoire  :

Latitude : 42,58+cosinus 74 ×47×360/40000 = 42,7° ou 42°42'.
Longitude : -5,57+sinus 74 ×47×360/(40000×cosinus 42,58) = -5,02° ou 5°01'W.

Avec le peu de données que nous avons, il n'y a guère d'autre solution que de procéder par tâtonnements...

Nous avons parlé des orbites elliptiques ou paraboliques suivies par les corps orbitant autour du Soleil... Il est temps de placer la Terre au centre de nos préoccupations, ce qui change quelque peut le statut de l'objet : il ne s'agit plus d'un satellite, objet en orbite, puisqu'il provient de l'espace lointain (à l'échelle de la Terre) avec une vitesse d'approche non nulle, supposée égale à 20 km/s.

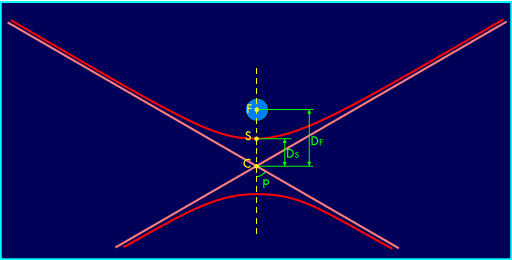
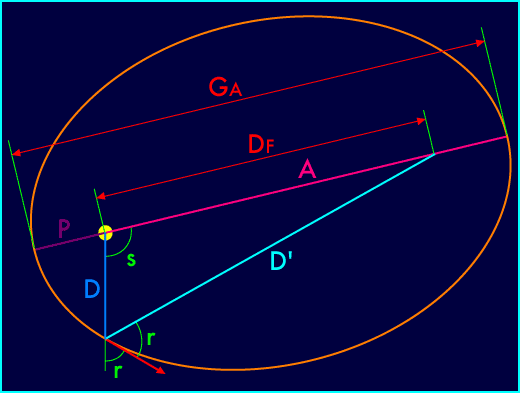
Dans ce cas, l'orbite suivie est une hyperbole :


Tout comme une ellipse, une hyperbole a deux foyers et deux sommets... En fait, nous avons vu qu'une ellipse devenait une parabole lorsque le second foyer et le second sommet (l'apoastre d'une orbite) s'éloignent à l'infini... Dans le cas d'une hyperbole, ils reviennent « par derrière » ! Une parabole est l'intermédiaire entre une hyperbole et une ellipse : ces trois courbes sont appelées « coniques » parce qu'elles correspondent à la section d'un cône par un plan (en mathématiques, un cône est « double », correspondant à la révolution dans l'espace d'une droite de longueur infinie en rotation ; l'hyperbole commence donc quand le plan de coupe traverse les deux parties opposés du cône).

Bien sûr, une seule moitié de l'hyperbole est suivie par l'objet, puisque l'autre moitié est en quelque sorte « au-delà de l'infini »... Notons au passage que puisque la force d'attraction est inversement proportionnelle au carré de la distance, un objet qui revient d'au-delà de l'infini subira la même force mais dans le sens opposé : de fait, cette seconde moitié de l'hyperbole est celle que suivrait un objet sur lequel la Terre exercerait une force de répulsion et non d'attraction, de même intensité... Voilà donc la recette de l'antigravitation, il suffit d'aller plus loin que l'infini !

Les deux droites qui se coupent au centre de l'hyperbole sont les « asymptotes », vers lesquelles les deux branches de la courbe tendent en s'éloignant du centre. On sera particulièrement intéressé par l'angle p entre l'axe et les asymptotes, puisque c'est lui qui mesure la déviation de l'objet en raison de l'attraction terrestre. Cet angle se calcule facilement en fonction de la distance du sommet au centre (D_S) et celle du foyer au centre (D_F) :

p = arc cosinus(D_S/D_F)

La distance D_S est égale MG/V_I².

MG est le produit de la constante de gravitation universelle par la masse de la Terre ; on le connaît bien plus précisément que M et G séparés justement parce qu'il détermine les orbites. Il vaut 3,986.10¹¹ newtons.mètres carrés par kilogrammes dans le système international. Si on exprime tout en kilomètres pour simplifier les notations (il faut juste faire attention de respecter un système d'unités cohérent : en choisissant le kilomètre comme unité de distance tout en gardant la seconde comme unité de temps, on devra exprimer toutes les distances en kilomètres et les vitesses en kilomètres par seconde), il vaudra donc un million de fois moins, soit 398600.

Et V_I, la distance d'approche « à l'infini », nous l'avons estimée égale à 20 km/s. Nous trouvons donc dans notre exemple :

D_S = 398600/400 = 996 km...

Le paramètre sur lequel nous pouvons jouer dans un premier temps, celui sur lequel se feront les « tâtonnements », c'est le rayon du périgée R_P, égal à D_F-D_S. S'il est égal au rayon terrestre, le météore arrive sous une trajectoire « rasante » ; s'il est égal à zéro, il heurte la Terre perpendiculairement. Nous savons simplement que l'angle d'arrivée était faible, nous étions donc plus proche du premier cas que du second... Supposons donc que le périgée se trouvait à 6000 km du centre de la Terre. Cela nous donne :

D_F = D_S+R_P = 6996 km.
p = arc cosinus(D_S/D_F) = 81,8°.

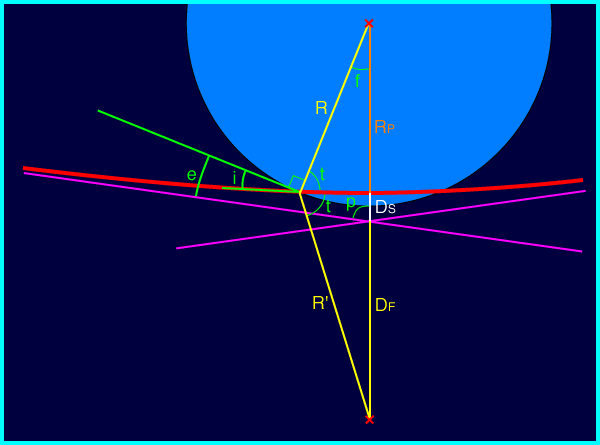
Ce qui nous intéresse, c'est de savoir comment se présentera la courbe lorsqu'elle passera par notre lieu de référence, à 6389 km du centre de la Terre (le rayon terrestre sous cette latitude, plus les 20 km d'altitude que nous avons considérés). Voyons pour cela comment les choses se présentent :


Une propriété des hyperboles est que la différence des distances aux foyers est égale à la distance entre les sommets (c'est presque la même règle pour les ellipses, chez qui c'est la somme et non la différence). D'où, ici :

R' = 2D_S+R = 8382 km

Nous avons donc les trois côtés du triangle représenté (le troisième étant 2D_F), ce qui nous permet de calculer l'angle f :

f = arc cosinus ((R²+(2D_F)²-R'²)/(2×R×2D_F)) = arc cosinus ((6389²+13992²-8382²)/(4×6389×6996)) = 21,5°.

Cette relation liant un angle d'un triangle quelconque aux trois côtés est très utile... Je ne la démontrerai pas, mais ça n'est pas trop difficile en prolongeant un côté du triangle afin de former un triangle rectangle.

Et de même, le sommet de gauche du triangle étant égal à 2t, on trouve :

t = 1/2×arc cosinus ((R²+R'²-(2D_F)²)/(2×R×R')) = 1/2×arc cosinus((6389²+8382²-13992²)/(2×6389×8382)) = 71,1°.

L'angle de descente i est égal à 90°-t = 18,9°... A priori, ça paraît assez raisonnable.

Un autre angle intéressant est l'angle e, entre l'asymptote d'arrivée et la tangente à la Terre :

e = p+f-90° = 81,8°+21,5°-90° = 13,3°.

Cet angle correspond à la hauteur angulaire du météore « à l'infini » (bien sûr, c'est une direction fictive puisqu'au-delà de l'atmosphère il n'y a plus de météore !) Et puisqu'on sait que l'asymptote d'arrivée doit-être parallèle à l'écliptique (ça n'est pas certain, mais au moins très probable), ça veut dire que cette hauteur sera la hauteur angulaire de l'écliptique à l'azimut correspondant à la direction d'arrivée du météore, juste à l'opposé de son « cap » !

Calculer cela demande un changement de coordonnées sphériques et c'est assez complexe, mais c'est tout à fait inutile puisque n'importe quel logiciel d'astronomie le fait très bien (ici par exemple MPJ Equinox) :


On voit que pour cette hauteur angulaire de 13,3°, l'écliptique passait à un azimut de 225,6°. Cela impliquerait donc un cap à 45,6°.

Si on veut être tout à fait précis, il faut tenir compte de la rotation de la Terre sur elle-même : le météore suit une orbite dont nous avons calculé les caractéristiques dans l'espace, mais le sol se déplace vers l'est à la vitesse d'un tour par jour... Le périmètre du parallèle 42°42' étant de 29400 km (40000×cosinus 42,7), ce déplacement vers l'est est de 29400/86160 = 0,34 km/s, et entraînera donc un décalage de la trace vers l'ouest.

Bien sûr, il faut connaître la vitesse du météore... Et elle se détermine facilement :

V = √(V_I²+V_E²).

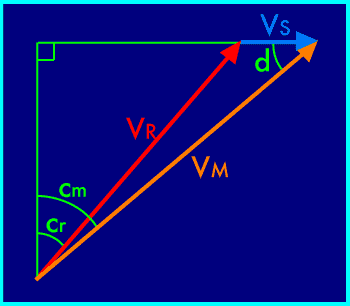
V_I, c'est la vitesse «à l'infini» que nous avons considérée égale à 20 km/s, et V_E c'est la vitesse d'évasion terrestre, égale à 11,2 km/s près du sol. La vitesse du météore sera donc égale dans notre hypothèse à 22,9 km/s. Et pour trouver la vitesse et le cap réels par rapport au sol, il faut à nouveau calculer une résultante de vitesses :


L'angle d est égal à 90°-C_M (le cap de l'astéroïde que l'on connaît), et on doit donc trouver le côté inconnu du triangle, correspondant à la vitesse relative, à partir des deux autres côtés et de l'angle qui les sépare... C'est donné par une autre formule pratique concernant les triangles, en fait l'inverse de celle que nous avons déjà utilisée, une généralisation du théorème de pythagore :

VR = √(V_M²+V_S²-2×V_M×V_S×cosinus d) = (22,9²+0,34²-2×22,9×0,34xcosinus(90-45,6)) = 22,7 km/s.

Le cap relatif pourrait ensuite être trouvé par la formule déjà vue donnant les angles d'un triangle dont on connaît les trois côtés, mais on peut remarquer plus simplement :

V_R×cosinus C_R = V_M×cosinus C_M
⇒ C_R = arc cosinus(V_M/V_R×cosinus C_M) = arc cosinus(22,9/22,7×cosinus 45,6) = 45°.

Il reste à voir si cette supposition d'un cap à 45° et un angle de descente de 18,9° est compatible avec la vidéo prise à León...

La vidéo qui tombe à pic

Sur cette vidéo, la présence de la lune nous donne un repère essentiel, puisqu'on sait qu'elle se trouvait à un azimut de 78,3° et une hauteur angulaire de 22,6°...

Il reste à déterminer l'échelle des angles. La lune pourrait encore nous l'indiquer puisque son diamètre est d'un demi-degré, mais elle apparaît trop petite sur la vidéo pour être exploitable... Tout au plus peut-on estimer qu'elle occupe environ deux pixels.

Mais cette vidéo décidément inespérée comporte une séquence beaucoup plus intéressante de ce point de vue, lorsque les rues sont filmées avant l'apparition du phénomène. Voici deux images extraites de cette séquence :


Sur la première, le vidéaste fait face au mur d'angle d'un bâtiment, et sur la seconde il filme dans l'axe de la rue qui longe ce bâtiment. On peut déterminer exactement à quel point de l'image correspond une vue du mur perpendiculaire grâce au store du bar, qui présente des bandes verticales. Et on peut aussi savoir précisément à quel angle correspond l'axe de la rue, il suffit de voir où se rencontrent les lignes prolongeant les trottoirs... Il reste à savoir à quelle différence d'angle de vue cela correspond, et ça dépend de l'angle entre les deux rues... En général, des murs d'angle tels qu'on en voit ici n'existent que lorsque les angles sont inférieurs à 90°... Faisons donc l'hypothèse qu'il soit de 60°, et nous essaierons de la vérifier ensuite. Il y aurait alors 30° entre l'axe de la rue et la perpendiculaire au mur d'angle :


Sur la vidéo telle qu'elle a été diffusée sur Internet, ces positions sont séparées par 173 points (le double sur ces extraits photographiques, que j'ai reproduits à l'échelle 2) ; chaque point correspondrait alors à 0,173°, ce qui s'accorderait bien avec la dimension de la lune, et la diagonale de l'image serait de 51°, un angle de champ courant pour un caméscope.

Tentons tout de même de vérifier notre hypothèse en portant notre attention sur les stores sur la deuxième photo :


L'extrémité gauche du store du mur d'angle s'écarte d'à peu près 6 points vers la gauche en s'éloignant du mur, et elle se trouve à peu près à 65 points de la perpendiculaire au mur. Elle serait donc vue sous une perspective de 65×0,173 = 11°, et sa longueur réelle, si le store était vu de profil, serait de 6/sinus 11 = 31 points.

L'autre store, qui serait incliné par rapport au premier de 60°, s'écarte du mur d'environ 26 points. La perspective serait donc de 60+26×0,173 = 64°, et la longueur réelle serait 26/sinus 64 = 29 points.

On peut donc affirmer sans risque de se tromper que notre estimation ne peut pas être très éloignée de la réalité. Il n'y a plus qu'à reporter le passage du météore à plusieurs instants sur une image et à mesurer les distances par rapport à la lune... On peut constater au passage que la photo qui a été diffusée indépendamment n'a pas tout à fait les mêmes proportions (352/288 points, soit un rapport de 1,22) que la vidéo ! J'ai supposé que les proportions correctes étaient celles de la vidéo (images de 234/180 points, rapport égal à 1,3) parce qu'elles m'ont paru plus conforme aux standards vidéo (proportions 4/3, soit 1,33), mais de telles incertitudes ne facilitent pas la tâche !

Voici donc ce que j'ai obtenu :


Notons que Ricardo Chao Priesto, de l'Asociación Leonesa de Astronomía, a obtenu des résultats sensiblement différents, comme on peut le voir sur cette image diffusée par la Sociedad de observadores de meteoros y cometas de España :


Il trouve un décalage en azimut de 15° là où j'en trouve 9, et en hauteur de 16° là où j'en trouve 11 (notons que les proportions du bâtiment sur sa photo sont les mêmes que sur la vidéo). Cette estimation « concurrente » (et spécifiée « provisoire » dans le texte) repose peut-être sur la supposition que les rues filmées avant le phénomène se coupent à angle droit, mais outre les considérations géométriques détaillées concernant les stores elle impliquerait un angle de champ anormalement élevé pour un caméscope... Je conserve donc ma propre estimation, en précisant tout de même qu'elle est incertaine...

De l'apparence à la réalité

Occupons-nous pour l'instant de l'angle de descente apparent, en espérant que les proportions sur la vidéo sont correctes : il est de 56,6° par rapport à l'horizontale (la décimale est un peu superflue)...

Il reste à étudier la perspective pour savoir quel était l'angle de descente réel du météore. Pour éviter d'avoir à tenir compte de la rotondité de la Terre, nous utiliserons comme repère les coordonnées de la lune vue depuis le point de survol qui nous sert de référence : hauteur 22,8° et azimut 78,7° (les coordonnées sur la photo sont données depuis la ville de León, donc un peu différentes)... Nous aurons ainsi les directions telles qu'elles seraient depuis le point d'observation situé dans un plan parallèle à l'horizontale du point de survol.

Considérons le météore dans sa position moyenne. La hauteur sur l'horizon est à peu près celle de la Lune, soit 23,1°, et l'azimut est inférieur de 4,7° à celui de la Lune, environ 74° (les mesures doivent se faire relativement à la lune et non par rapport aux indications de la grille, ces dernières correspondant aux coordonnées célestes à León).

Nous avons supposé que le météore suivait un cap de 45° avec un angle de descente de 18,9°... Voyons donc quel angle de descente apparent cela donnerait pour un observateur qui regarderait à un azimut de 74° et à une hauteur angulaire de 23,1° :


Bien sûr, tous les déplacements sont grossis pour que l'on puisse les visualiser, mais ils doivent être très petits par rapport à la distance de l'observateur... En fait, il s'agit d'analyser les directions en un point.

L'angle a est la différence entre la direction de l'observation (azimut 74°) et celle du plan de l'orbite (azimut 45°) : il sera donc égal à 29°. Il s'agit bien d'un angle qui doit être mesuré sur un plan horizontal, puisque l'azimut est la direction par rapport à l'horizon.

Pour décomposer le mouvement, j'ai considéré que l'objet se déplaçait d'abord d'une distance X sur un plan parallèle à la Terre, puis descendait verticalement. Cela permet de garder constant le déplacement vers la gauche.

Pour un déplacement de l'objet égal à X, le déplacement vers la gauche sera :

X×sinus a.

Et le déplacement vers le bas :

X×cosinus a ×sinus h +X×tangente i ×cosinus h.

D'où on tire l'angle de descente apparent :

sinus d /cosinus d = tangente d = sinus h /tangente a +tangente i ×cosinus h /sinus a.

Il ne reste plus qu'à remplacer par les valeurs connues h = 23,1°, a = 29° et i = 18,9° :

d = arc tangente (sinus 23,1 /tangente 29 +tangente 18,9 ×cosinus 23 /sinus 29) = 53,6°.

On devrait trouver 56,6°, ça n'est pas tout à fait ça mais on n'est pas loin... Il n'y a plus qu'à recommencer depuis le début avec une nouvelle valeur pour le périgée... Et recommencer encore jusqu'à ce qu'on trouve les 56,6° désirés. Je vous avais dit qu'il faudrait tâtonner...

Un tableur à notre secours...

Bien sûr, depuis que les ordinateurs existent, ils peuvent se charger des tâtonnements à notre place ! Pour cela, soit on écrit un programme qui fait tous les calculs à partir des données initiales, soit on utilise un tableur.

J'ai une préférence pour la première solution, ayant connu les temps heureux où tous les ordinateurs étaient vendus avec un langage de programmation, et où on apprenait donc nécessairement à programmer... Ces temps sont maintenant révolus, et de nos jours bien peu d'utilisateurs d'ordinateurs savent faire autre chose qu'utiliser des programmes tout faits (ce qui est souvent bien plus compliqué que de faire son propre programme pour des applications très spécifiques). Pour ne pas restreindre encore le nombre de lecteurs qui me suivront, j'ai préféré faire appel à un tableur, bien que je n'en aie pas l'habitude.

Vous pouvez donc vous amuser à faire varier l'orbite à volonté en changeant les paramètres variables sur cette feuille de calcul Excel...

Le tableur fait automatiquement tous les calculs que nous avons détaillés, et modifie instantanément les résultats si on change les paramètres de base : la vitesse à l'infini, le rayon du périgée et l'altitude lors du passage au point de référence. Je ne détaillerai pas tout, ceux qui veulent savoir ce qu'il fait précisément pourront examiner les formules utilisées dans les cellules de calcul.

Une remarque au passage : les tableurs, comme la plupart des langages de programmation, utilisent le radian comme unité d'angle... C'est en effet la façon la plus naturelle d'exprimer un angle : elle correspond à la longueur de l'arc de cercle par rapport au rayon... Un tour complet correspond donc à 2π radians... Ça ne complique pas non plus l'énoncé des angles « ronds », si l'on peut dire, puisqu'il n'est pas plus facile de dire par exemple soixante degrés plutôt que π/3 radians. La deuxième notation est même beaucoup plus parlante puisqu'on sait tout de suite qu'il faut trois angles identiques pour totaliser 180 degrés, pardon π radians. Bref tout serait beaucoup plus simple si on apprenait à exprimer les angles en radians plutôt qu'en degrés. Le radian est d'ailleurs l'unité légale des angles dans le système international, celui que tout le monde devrait utiliser. Malheureusement, on apprend toujours à l'école à utiliser les degrés, cette unité héritée des temps barbares où l'on ignorait la valeur de π... Mais j'ai déjà suffisamment bousculé les habitudes en introduisant le gigamètre, j'ai donc préféré conserver les degrés, bien que toutes ces conversions alourdissent les formules.

Dans les calculs que nous avons déjà effectués, nous avons utilisé un logiciel d'astronomie pour connaître la direction d'arrivée du météore en fonction de la hauteur sur l'écliptique calculée... Bien sûr, on ne peut pas s'amuser à recommencer à chaque fois que l'on change une donnée pour voir ce que ça donne... Voyons donc comment on peut le calculer automatiquement, sans pour autant nous lancer dans des calculs complexes de changement de coordonnées :


Ce que l'on cherche, c'est l'angle a. Ce que l'on connaît, c'est l'angle h. L'angle i, inclinaison de l'écliptique par rapport à l'horizon, est égal à la hauteur maximale de l'écliptique, que l'on peut rechercher avec le logiciel d'astronomie :


Elle se situe ici près de la planète Mars, et cette hauteur angulaire est de 47,8°.

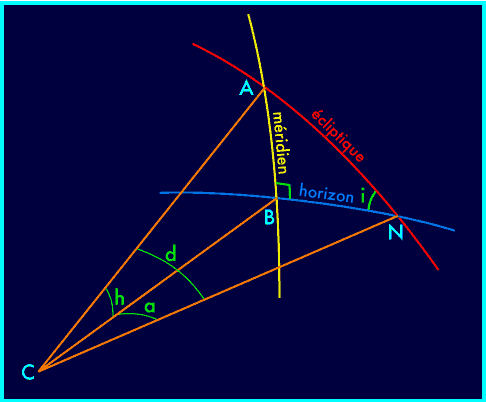
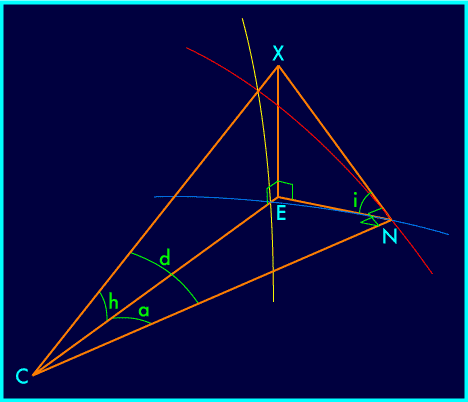
Il s'agit donc de trouver l'angle a à partir de h et de i. Ce genre de problème de géométrie sphérique se résout facilement par la trigonométrie classique en essayant de constituer avec tous les angles connus ou à connaître un tétraèdre formé de triangles rectangles... Trois des triangles seront respectivement dans le plan de l'horizon, du méridien et de l'écliptique... Le quatrième devra être choisi tangent à la sphère en N, afin qu'il intègre l'angle i :


Ce triangle sera ainsi perpendiculaire à ceux situés sur les plans de l'horizon et de l'écliptique, et d'autre part le segment EX sera à l'intersection de deux plans perpendiculaires à l'horizon, il lui sera donc également perpendiculaire. Notre tétraèdre est donc bien composé uniquement de triangles rectangles, et il suffit d'utiliser les notions de trigonométrie classique pour passer d'une valeur à l'autre :

tangente a = EN/CN
EN = EX/tangente i
EX = EC×tangente h
EC = CN/cosinus a

Et donc :

tangente a = CN/cosinus a ×tangente h /tangente i /CN
⇒ tangente a ×cosinus a = tangente h /tangente i
⇒ a = arc sinus(tangente h /tangente i).

C'est ce que vous trouvez dans la feuille de calcul dans la cellule B21, pour le calcul du « cap ».

D'autre part, le tableur calcule automatiquement les coordonnées du « point de référence » en fonction de la distance obtenue depuis León... Cette valeur change avec l'altitude en ce point... Si on modifie beaucoup l'altitude et si on veut des calculs précis, il sera donc nécessaire de revoir les données calculées par le logiciel d'astronomie en modifiant le lieu d'observation.

Les données qui nous seront utiles sont :

— la position de l'écliptique lorsqu'elle coupe l'horizon à l'est (on appelle ces positions les « noeuds ») ;

— la hauteur maximale de l'écliptique, égale à son inclinaison par rapport à l'horizontale du lieu de référence, dont nous venons de parler ;

— les coordonnées de la lune (hauteur et azimut) ;

— plus loin, nous aurons besoin de la position du soleil sur l'écliptique... Le plus simple est de mesurer encore sa hauteur sur l'horizon, puisque nous savons maintenant calculer le reste : elle est égale à 1,1°.

Nous verrons plus loin d'autre calculs utilisés dans la feuille de calculs...

Recherche de compromis

Essayons maintenant de jouer un peu avec ces calculs... Le but est donc de faire varier les paramètres de base jusqu'à ce que l'angle de descente théorique s'accorde avec celui, mesuré sur la vidéo, de 56,6°...

Essayons d'abord de conserver la vitesse à l'infini de 20 km/s et de faire varier uniquement le rayon au périgée : on obtient le bon angle de descente pour un périgée à 6234 km. Les autres paramètres obtenus sont : angle de descente 11,9°, cap 52,4°. Ça paraît raisonnable...

Essayons maintenant de faire varier la vitesse, par exemple avec 15 et 25 km/s.

Dans le premier cas, on obtient, pour un rayon au périgée de 5944 km, un angle de descente de 19,5° et un cap à 47,5°.

Dans le second, pour un rayon au périgée de 6303 km, un angle de descente de 9° et un cap à 53,4°.

Cherchons maintenant les valeurs limites : à partir d'une vitesse à l'infini de 31 km/s, le périgée doit être au-dessus du rayon terrestre, ce qui implique que le météore n'atteint pas le sol et repart dans l'espace (si on ne tient pas compte du freinage atmosphérique). Le cap est de 57,4°, l'angle de descente de 3,5° seulement. Tout ça serait parfaitement compatible avec la trajectoire d'un météore de nature cométaire qui se serait approché de la Terre sous une trajectoire parabolique. Ça n'est pas franchement exclu, mais c'est difficile à concilier avec les témoignages qui semblent indiquer une descente relativement rapide et une trajectoire dans l'atmosphère assez courte... Sous une telle trajectoire « rasante », le météore aurait parcouru près d'un millier de kilomètres à moins de 150 km d'altitude avant de passer à proximité de León, et ça n'est pas ce que les témoignages suggèrent... Notamment, la mention d'une détonation est vraiment restreinte à la région de León. Enfin, il est extrêmement improbable qu'un objet suive une telle trajectoire « rasante ».

Si au contraire on diminue la vitesse, on se rend compte qu'elle doit être d'au moins 5,7 km/s pour que l'on puisse respecter l'angle de descente montré sur la vidéo, avec un cap à 0° (plein nord)... Mais l'angle de descente réel est alors presque identique, égal à 55,9° : ça signifie que la trajectoire du météore est perpendiculaire au témoin, mais c'est cette fois en opposition totale avec les témoignages, qui indiquent un angle de descente assez faible.

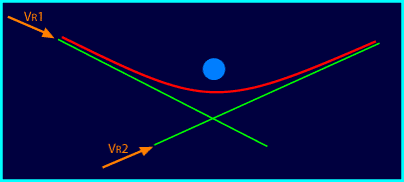
Notons d'ailleurs qu'une telle trajectoire très inclinée est possible à toutes les vitesses : il y a en réalité deux possibilités pour une vitesse donnée, qui deviennent identiques pour 5,7 km/s; par exemple pour 20 km/s on trouve aussi une trajectoire conforme à la vidéo avec un périgée à 3865 km du centre de la Terre, impliquant un angle de descente de 49,4° et un cap à 16,2°... Mais c'est bien entendu à exclure dans le cas qui nous concerne.

Nous arrivons donc à la conclusion que tout un éventail de conditions initiales peuvent correspondre à la vidéo... Il nous manque un élément pour choisir celle qui convient le mieux.

Les paramètres qui varient sont le cap et l'angle de descente. N'ayant pas d'éléments pour estimer précisément le premier, on peut se rabattre sur le second en se fiant à la photographie prise par Salvador Diez (Red de Investigacion sobre Bólidos y Meteoritos) dans les environs de León :


L'angle de descente est de 13,5°... Bien sûr, il s'agit d'un angle apparent, qui ne correspond à l'angle réel que si l'appareil photo était tenu bien droit et si la photo a été prise quand le météore passait au plus près... Sur le premier point, on ne peut qu'espérer que le photographe est plus doué que moi, qui ai toujours quelques problèmes pour obtenir des photographies droites ! Et sur le second on doit aussi espérer... Il ne semble pas en tout cas que l'objet ait dépassé de beaucoup son passage au plus près, sans quoi le photographe aurait le soleil dans le dos et les rochers seraient éclairés, et s'il n'a pris qu'une photo on peut supposer qu'il a attendu que l'objet passe au plus près... On manque d'éléments pour apprécier la direction du soleil, mais rien ne permet d'exclure une direction de visée à environ 130° (le cap suivi par le météore plus 90°) pour un soleil situé à 240°, bien à droite. Bref il semble raisonnable de penser que l'on peut se fier, au moins grossièrement, à cet angle de descente.

Essayons donc d'obtenir cet angle avec le météore lorsqu'il passe à proximité de León.

Pour que les calculs soient précis (ça n'est pas vraiment utile quand les données ne le sont pas, mais faisons comme si...), nous devons connaître l'angle de descente à proximité de León, et non à l'endroit que survolait le météore quand il était filmé. La distance entre le point de référence et León a déjà été estimée d'après l'altitude supposée... D'autre part, nous savons déjà comment calculer les paramètres tels que l'angle de descente d'après la distance au centre de la Terre. Estimons donc dans un premier temps à quelle altitude passe le météore à proximité de León, d'après son angle de descente au point de référence : ça sera la distance au sol multipliée par la tangente de l'inclinaison, ajoutée à l'altitude au point de référence.

Avec ça, on peut calculer toutes les autres valeurs, notamment l'angle de descente précis, comme on l'a déjà fait.

Et on trouve donc un angle de descente près de León égal à 13,4° pour une vitesse à l'infini égale à 19 km/s, et un rayon au périgée égal à 6199 km. Le cap est alors de 52,2 degrés.

Vitesse apparente

On peut encore chercher à savoir si la vitesse de déplacement est compatible avec celle de la vidéo... Bien sûr, ça ne sera qu'approximatif puisque la vitesse d'arrivée n'est pas connue précisément (elle dépend de la vitesse à l'infini), que la vitesse angulaire calculée d'après la vidéo est très imprécise, et qu'à l'altitude considérée le freinage atmosphérique doit être important...

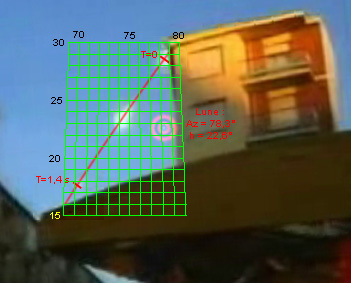
Reprenons le schéma de calcul des angles sur la vidéo :


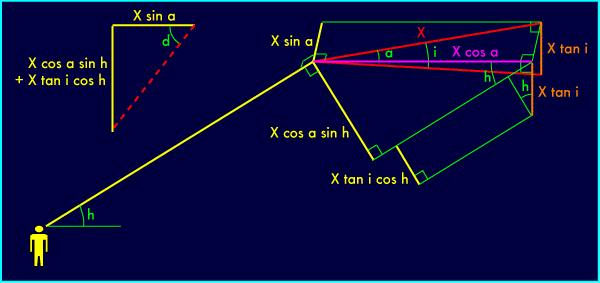
Le plus simple est de considérer uniquement le déplacement apparent latéral parcouru entre les deux points extrêmes (séparés par 1,4 s)... On connaît la vitesse supposée du météore ; en la multipliant par la durée de 1,4 seconde, on obtient la distance parcourue ; en la multipliant par le cosinus de l'angle de descente i, on obtient cette distance projetée sur un plan horizontal (X sur le schéma) ; en la multipliant encore par le sinus de l'angle a, égal à la différence entre le cap et la direction d'observation, on obtient le déplacement apparent latéral. Ce qui nous intéresse, c'est le déplacement du météore en azimut, qui sera l'angle correspondant au déplacement latéral divisé par le cosinus de la hauteur angulaire (l'azimut correspond à la longitude sur la sphère céleste, alors que la hauteur correspond à la latitude ; on doit donc appliquer la même conversion que quand on veut calculer une différence de longitude par rapport à une distance). Nous avons donc :

DA = arc sinus (V×1,4×cosinus i ×sinus a)/d/cosinus h.

Avec les valeurs calculées, on obtient :

DA = arc sin(21,8×1,4×cosinus 13,1×sin 22,3)/51/cos 23,1 = 13,9 degrés.

À comparer avec la variation d'azimut sur la vidéo, égale à 8° :


Si l'on voulait faire correspondre les deux valeurs, il suffirait de considérer que le météore était plus loin de León que nous ne l'avons supposé, et augmenter l'altitude... Mais en fait, on sait qu'il doit avoir considérablement ralenti en raison du freinage atmosphérique : il est difficile d'estimer ce ralentissement, qui dépend essentiellement du volume de l'astéroïde et de la façon dont il se réduit et se fragmente, mais on peut estimer qu'une perte de 40% de la vitesse initiale est très acceptable à une altitude de 20 km.

Nous conserverons donc cette altitude pour le météore lorsqu'il était filmé, puisqu'elle s'accorde assez bien avec les témoignages...

Notons que si le freinage atmosphérique peut diminuer considérablement la vitesse en fin de parcours, il n'a que peu d'effet sur la trajectoire et l'angle de descente pour une distance parcourue en quelques secondes.

Trajectoire

Venons-en justement à la trajectoire. Pour la tracer, nous avons déjà le point de référence choisi, correspondant au passage filmé : 42°42'N, 5°01'W.

Le point le plus intéressant est bien sûr celui de l'impact, si impact il y a eu : il correspond au moment où la distance de l'hyperbole au centre de la Terre est égale au rayon terrestre, soit 6369 km dans cette région.

Nous avons déjà vu comment calculer l'angle entre le rayon où se trouve l'objet et le périgée, il suffit donc de recommencer avec un rayon égal au rayon terrestre pour connaître le nouvel angle, et en faisant la différence, on obtiendra l'angle séparant sur le globe terrestre le point d'impact de notre point de référence.

La distance séparant ces deux points, ça sera cet angle multiplié par la circonférence terrestre et divisé par 360°...

On peut encore estimer la durée de ce parcours, en divisant cette distance par la vitesse. Pour être précis, on devrait tenir compte de la variation de vitesse et d'altitude, et calculer en fait la surface de la portion d'hyperbole balayée (une des lois découvertes par Kepler, et expliquées plus tard par Newton, est que le « rayon vecteur » d'un objet en orbite balaie des aires égales en des temps égaux). Ça compliquerait inutilement les calculs, et on peut se contenter d'une estimation pour une altitude qui ne varie pas beaucoup.

En l'occurrence, on trouve une distance de 88 km séparant le point de référence du point d'impact, parcourue en 4,1 s.

Outre ce temps, ce qui nous intéresse n'est pas tellement la distance séparant les deux points, mais de pouvoir calculer les coordonnées géographiques du second... On se trouve devant un problème de géographie classique, consistant à trouver les coordonnées d'une ville d'arrivée à partir de celles de la ville de départ, de la distance qui les sépare et de la direction à suivre (en fait, on est plus souvent confronté au problème inverse). C'est encore un problème de géométrie sphérique, on peut trouver la solution par la trigonométrie classique en choisissant judicieusement les triangles liant les différentes valeurs connues ou à trouver, mais c'est assez complexe (il ne s'agit pas cette fois d'un simple problème de triangle sphérique, puisque les écarts en longitude ne sont pas mesurés à partir du centre de la sphère) et je vous ai déjà imposé suffisamment (sûrement beaucoup trop pour certains !) de calculs. Si ça vous intéresse, vous pourrez chercher les formules à utiliser dans les cellules concernées de la feuille de calcul.

Notez que l'on doit tenir compte pour être précis du déplacement du sol vers l'est sous le météore, diminuant le déplacement en longitude (et ne pas utiliser la valeur corrigée du cap tenant déjà compte de ce déplacement, qui n'est valable qu'à un instant précis). Il est facile à calculer à partir de la durée, puisque le sol parcourt 360° de longitude en 24 h.

On trouve un point d'impact estimé à 43°11'N et 4°10'W. Il sera à rechercher en réalité un peu avant, en tenant compte du ralentissement dû à l'atmosphère.

Un autre instant intéressant est celui où le météore est devenu visible par sa luminosité, à une altitude que l'on peut estimer à 150 km... Il s'agit donc de refaire les mêmes calculs pour une distance au centre de la Terre égale au rayon terrestre plus 150 km. On trouve cette fois une distance de 480 km (dans l'autre sens bien sûr), parcourue en 26,6 s. Le point survolé est à 39°58'N et 9°33'W.

On peut enfin chercher de la même manière le point situé à proximité de la ville de León, après avoir estimé l'altitude de passage... On trouve 42°27'N et -5°35'W, à 6,3 s de l'impact. Le temps écoulé entre le passage au plus près de León et le moment où le météore a été filmé serait donc de seulement 2,2 s, en fait un peu plus en tenant compte du freinage atmosphérique...

Le temps de visibilité total serait de l'ordre de 30 s, exceptionnel pour un météore... Toutefois, il ne pouvait sûrement pas être vu à une altitude de 150 km dans les régions où il faisait jour, si bien que la durée possible d'observation ne devait pas dépasser une quinzaine de secondes.

Notons que ces considérations rendent un peu douteuse la possibilité d'observation du météore depuis le Cannet, puisque le point de rentrée dans l'atmosphère estimé se trouve à 1430 km de cette ville et que la distance de visibilité d'un objet à 150 km d'altitude n'est que de 1390 km... Mais cette distance théorique doit être un peu augmentée en tenant compte de la réfraction atmosphérique, et l'altitude de 150 km à laquelle j'ai supposé que le météore devenait visible (pour un observateur situé dans la nuit) est assez variable... Cette observation au Cannet, qui n'est de toute façon pas attestée sérieusement, n'est donc pas totalement incompatible avec les paramètres que nous avons retenus, lesquels sont aussi très incertains.

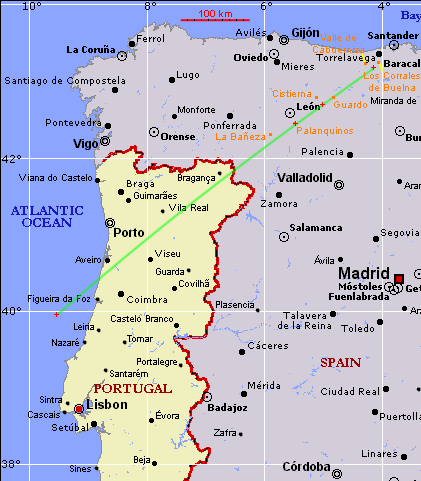
Voici le tracé au sol de la trajectoire que nous obtenons :


Je rappelle que cette trajectoire n'est rien d'autre qu'un petit exercice théorique, obtenu uniquement à partir d'une courte séquence vidéo et une photographie... Il est inutile de vous précipiter en Espagne pour rechercher des météorites à l'endroit précis de l'impact ! Les astronomes espagnols qui étudient cette affaire disposent de bien plus de données et sont certainement plus compétents que nous pour estimer la trajectoire réelle... Nous aborderons à la fin les indications qu'ils ont déjà données à ce sujet.

Orbite autour du Soleil

Si l'on disposait de témoignages vraiment très précis, on pourrait non seulement reconstituer la trajectoire au sol de ce petit astéroïde, mais aussi son orbite avant qu'il ne rencontre notre planète... Nous allons voir comment on fait, en sachant bien que les résultats seront très hasardeux...

Il s'agit dans un premier temps de connaître la vitesse et la direction de l'astéroïde avant qu'il n'approche de la Terre... Ce que nous connaissons, c'est la vitesse de la Terre sur son orbite et la vitesse de l'astéroïde relativement à la Terre, mais nous ne connaissons pas encore la direction d'où provient l'objet par rapport au Soleil.

Nous avons juste supposé que cette direction se situe dans le plan de l'écliptique, et nous connaissons sa hauteur sur l'horizon, égale à 6,3° dans l'hypothèse choisie (c'est l'angle « HA » de la cellule B17 sur la feuille de calcul). Nous avons déjà vu comment calculer l'azimut à partir de cette hauteur, il s'agit cette fois de calculer l'angle parcouru sur l'écliptique, celui qui correspond à « l'hypothénuse » du triangle sphérique (en rouge) :


Nous connaissons donc les angles h et i, et il nous faut cette fois trouver d :

CE = CX×cosinus h
EX = CE×tangente h
XN = EX/sinus i = CX×sinus d.

d'où :

sinus d = CX×cosinus h ×tangente  h /(CX×sinus i) = sinus h /sinus i
d = arc sinus (sinus h /sinus i) = arc sinus (sinus 6,3 /sinus 47,8) = 8,6°.

Ce que nous cherchons, c'est la distance angulaire séparant ce point de la position du Soleil sur l'écliptique... Il suffit donc de faire la même chose avec la position du soleil, dont nous savons par le logiciel d'astronomie qu'il se trouve à une hauteur de 1,1°.

L'angle entre la direction du Soleil et la direction d'arrivée de l'astéroïde sera donc :

g = 8,6°-arc sinus (sinus 1,1 /sinus 47,8) = 7,1°.

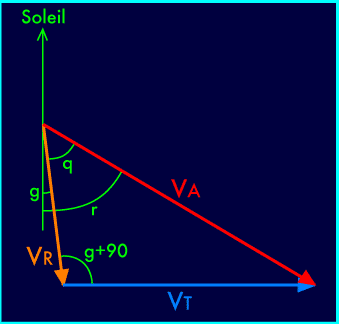
Nous pouvons maintenant calculer la vitesse de l'astéroïde sur son orbite au moment où il croise celle de la Terre, d'après le triangle formé par les vitesses de la Terre et de l'astéroïde et la vitesse résultante :


Nous connaissons V_T, vitesse de la Terre sur son orbite, égale à 29,8 km/s, V_R, la vitesse relative, égale à la vitesse « à l'infini » de la trajectoire hyperbolique, que nous avons estimée égale à 19 km/s, et l'angle g que nous venons de calculer, égal à 7,8°.

Il ne reste plus qu'à appliquer les formules classiques sur les triangles pour trouver le reste :

V_A = √(V_R²+V_T²-2×V_R×V_T×cosinus(g+90))
= √(19²+29,8²-2×19×29,8×cosinus(97,8)) = 37,3 km/s.
q = arc cosinus((V_R²+V_A²-V_T²)/(2×V_R×V_A))
= arc cosinus((19²+37,3²-29,8²)/(2×19×37,3)) = 52,5°.
r = q+g = 59,6°.

C'est cet angle r, entre la direction suivie par l'astéroïde et la direction du Soleil, qui nous sera utile pour la suite : avec lui, la vitesse de l'astéroïde et la distance du Soleil (égale à celle de la Terre au Soleil), nous pouvons reconstituer entièrement l'orbite :


Quelle que soit la direction du déplacement, le grand axe d'une orbite est toujours déterminé par la vitesse en un point quelconque, selon la formule :

G_A = 2D/(2-(V/V_C)²)

Ici, D est le rayon de l'orbite terrestre, 150 Gm (gigamètres, je le rappelle), V est la vitesse de l'astéroïde, égale à 37,3 km/s, et V_C, la vitesse de satellisation circulaire, est bien entendu la vitesse de la Terre sur son orbite, égale à 29,8 km/s. D'où :

G_A = 2×149,6/(2-(37,3/29,8)²) = 686 Gm.

Sachant que le carré du temps de révolution est proportionnel au cube du grand-axe, il est facile d'en déduire la durée de l'orbite d'après celle de la Terre (365 jours) : on trouve 1268 jours.

Par ailleurs, une propriété des ellipses est que la somme des distances séparant un point des deux foyers est égale au grand-axe :

D' = G_A-D.

Une autre propriété bien connue est qu'un rayon partant d'un foyer est réfléchi sur le second... En clair, cela signifie que la tangente à l'ellipse, soit la direction du déplacement de l'astéroïde, forme un angle identique avec les droites D et D' ; et cet angle, on le connaît, c'est l'angle r égal à 59,6°.

À partir de là, on peut trouver tous les paramètres qui nous manquent en appliquant les relations déjà vues concernant les triangles :

D_F = √(D²+(G_A-D)²-2×D×(G_A-D)×cosinus(180°-2r)) = 481 Gm.
Périhélie = (G_A-D_F)/2 = 102 Gm.
Aphélie = (G_A+D_F)/2 = 584 Gm.
s = arc cosinus((D²+D_F²-(G_A-D)²)/(2×D×D_F)) = 103,5°.

Cet angle s permet de connaître l'orientation du grand axe de l'orbite par rapport aux étoiles, puisqu'on connaît l'orientation du rayon de l'orbite terrestre... Les seuls paramètres que nous n'avons pas déterminés concernent l'inclinaison de l'orbite par rapport à l'écliptique, qui n'est pas tout à fait nulle.

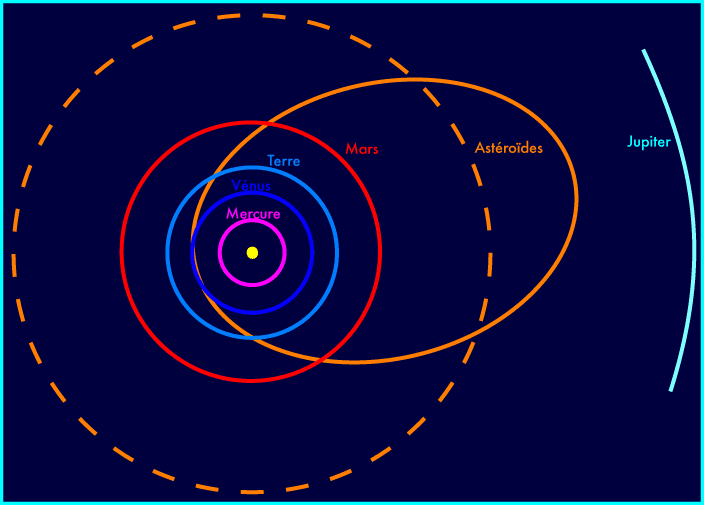
Voici comment se présenterait cette orbite par rapport aux planètes du système solaire :


Ça serait assez courant pour un astéroïde. Ceci dit, je rappelle que cette orbite ne correspond sûrement pas à la réalité, mais on peut espérer qu'elle ne s'en éloigne pas trop !

D'autre part, vous aurez peut-être trouvé un peu abusif que nous soyons passés sans transition d'une trajectoire hyperbolique à proximité de la Terre à une trajectoire elliptique autour du Soleil... Ça n'est bien sûr qu'une approximation, assez précise si les dimensions caractéristiques de l'orbite terrestre sont très inférieures à celles de l'orbite solaire... En fait, si les orbites suivies par deux corps en mouvement l'un autour de l'autre sont des courbes faciles à exprimer mathématiquement, dès que l'on fait intervenir un troisième corps ça n'est plus du tout le cas... Les calculs précis sont effectués par des ordinateurs qui calculent pas à pas ce qui se passe en tenant compte des différentes influences... On obtient ainsi une précision extrême pourvu que les « pas » soient réduits, mais on ne comprend pas ce qui se passe !

Considérer les courbes suivies comme une succession de courbes simples permet de comprendre les lois de la mécanique orbitale, par exemple « l'effet de fronde » permettant d'accélérer une sonde spatiale sans dépenser aucun carburant, en la faisant passer à côté d'une planète : la sonde arrive près de cette planète à une certaine vitesse relative, et elle la quitte, après avoir suivi une trajectoire hyperbolique, à la même vitesse mais dans une direction différente ; elle a donc été déviée d'une certaine vitesse, que l'on retrouve bien entendu sur la vitesse orbitale.

Dernières nouvelles d'Espagne

Depuis que j'ai commencé à rédiger cet article et à essayer de me familiariser avec les trajectoires de météores, plus d'une semaine s'est écoulée, et les astronomes espagnols ne sont pas restés inactifs. Le 14 janvier, la Red de Investigación Sobre Bólidos y Meteoritos (Spanish Fireball Network), qui s'est beaucoup impliquée dans cette recherche, annonçait une « trajectoire préliminaire » obtenue avec une équipe internationale de chercheurs : le Dr Josep María Trigo-Rodríguez de l'Institut de géophysique et de physique planétaire de l'Université de Californie de Los Angeles, le Dr Jose Luis Ortiz de l'Institut d'astrophysique d'Andalousie, le Dr Jordi Llorca Pique de l'Université de Barcelone et de l'Institut d’Études spéciales de Catalogne (IEEC) et le Dr José Angel Docobo de l'Observatoire astronomique Ramon Maria Aller de l'Université 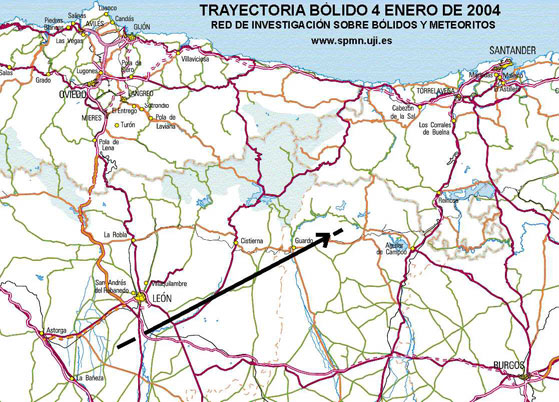de Saint-Jacques de Compostelle. J'ai rapporté cette trajectoire en rouge sur la mienne pour comparaision :


Le cap est pratiquement identique, la trajectoire annoncée par ce groupe passe juste un peu plus près de León que la mienne, à seulement quinze kilomètres au sud au lieu de 23. Par contre, son angle de descente est bien plus important, comme on le voit à sa faible longueur et comme le confirme le texte :

« La trajectoire déduite montre le bolide arriver au sud de la province de León, survoler cette ville à une altitude d'environ 80 km en direction de Guardo et éclater à 30 km d'altitude peu de temps après, au-dessus du nord de la province de Palencia. Les fragments ont continué leur descente, restant encore lumineux à moins de 20 km d'altitude. »

Cela supposerait un angle de descente de l'ordre de 35°. Je suis un peu perplexe, parce que je ne vois pas comment une trajectoire aussi inclinée pourrait s'accorder avec la vidéo tournée à León... D'autant que le cap donné par ces chercheurs, un peu plus incliné vers l'est que celui que je trouve, ne fait qu'empirer les choses : avec de telles données, la vidéo devrait montrer une trajectoire apparente presque verticale !

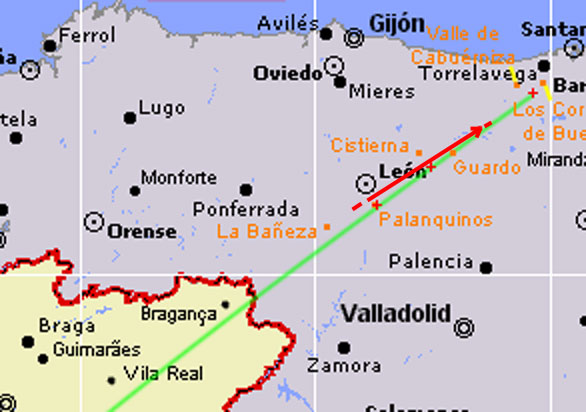
Juste après avoir édité la première version de cet article, j'ai appris par Éric Maillot que la trajectoire estimée avait été légèrement modifiée le 20 janvier (mais elle reste toujours « provisoire »). Voici la nouvelle carte (vous pouvez la voir en plus grand sur le site de la Red de Investigación Sobre Bólidos y Meteoritos) :


Ma perplexité ne fait que s'accroître, puisqu'avec un cap encore un peu dévié vers l'est et une distance parcourue un peu plus courte, l'incompatibilité avec l'angle de descente sur la vidéo ne fait que s'accroître ! Je ne serais pas surpris que ces chercheurs donnent volontairement une trajectoire un peu faussée afin de de ne pas attirer les curieux et les chasseurs de météorites sur le site d'impact, pour réserver la découverte de météorites aux scientifiques. Ça serait « de bonne guerre »...

Ces experts annoncent aussi que le fragment d'astéroïde a « pénétré dans l'atmosphère terrestre à une vitesse de 15±5 km/s » (revue depuis à 19±3 km/s). Avec les 22 km/s que j'ai obtenus, je serais un peu en dehors de cette fourchette. Toutefois, il est tout à fait impossible qu'un astéroïde touche l'atmosphère à moins de 11,2 km/s, et très exceptionnel que ce soit à moins de 15... Cette mention de « 15±5 » concernant la vitesse à l'entrée dans l'atmosphère me paraît donc aussi très suspecte... Je suis tenté de penser qu'elle se rapporte plutôt à la vitesse relative « à l'infini », et elle serait alors en bon accord (de plus en plus !) avec les 19 km/s que j'ai estimés.

Bref j'attendrai l'annonce d'une trajectoire qui ne soit plus « préliminaire » pour me faire une opinion...

La masse estimée du bolide serait de 10 tonnes au moins, et je suis arrivé précisément au même chiffre avec une vague estimation personnelle (je reparlerai bientôt de la façon de faire de telles estimations)... C'est aussi un bon compromis entre les 50 à 100 tonnes estimés initialement par un astronome espagnol et les quelques centaines de kilogrammes par son confrère portugais.

Ces chercheurs annoncent aussi qu'un lien semble pouvoir être fait avec un météore qui avait traversé le ciel de l'Oklahoma le 3 janvier 1970, laissant des météorites près de Lost City (un coin perdu comme son nom l'indique)... Nous verrons plus loin que c'est tout à fait exclu.

Concernant la recherche de météorites, le même site indique qu'il est très probable compte tenu des caractéristiques du météore que des fragments aient atteint le sol. En outre, deux fragments supposés ont bien été identifié comme une météorite, une « chondrite » banale composée essentiellement de roches et de fer... La chasse aux météorites continue donc.

Bref, cette affaire connaîtra certainement encore des développements intéressants, et encore une fois ce sont les témoignages qui permettent de préciser la trajectoire ou le point d'impact... Alors, si vous avez observé le phénomène, ou si vous connaissez quelqu'un qui l'a observé, faites-le savoir.

Jusqu'à présent, on n'a pu calculer les orbites que de six objets ayant laissé des météorites (le plus connu est celui de Peekskill, qui a achevé sa course sur une automobile, laquelle a ainsi pris beaucoup de valeur en devenant incapable de rouler !) Il se pourrait que le météore du 4 janvier devienne le septième...

Additif (25/01/2004) :

Orbites et écliptique

Les études concernant ce météore se poursuivent, et de mon côté je continue à parfaire mes connaissances dans ce domaine... En bref à me rendre compte de mes erreurs...

Depuis que j'ai mis en ligne ce texte (il y a seulement trois jours), le groupe de recherche espagnol du SPMN (Spanish fireball network, Red de investigación sobre bólidos y meteoritos), à qui je l'ai communiqué, a révisé la vitesse estimée de l'objet : 19±3 km/s au lieu des 15+-5 annoncés précédemment... Le texte n'ayant pas été modifié, on ignore si cette vitesse correspond cette fois à la vitesse d'entrée dans l'atmosphère comme c'est indiqué, ou à la vitesse « à l'infini » comme c'était manifestement le cas avec l'ancienne valeur. Le responsable de ce groupe et du site Internet, le Dr Josep Maria Trigo-Rodrigez, ne semble d'ailleurs pas désireux de clarifier les choses. Cette confusion entre vitesse d'impact sur l'atmosphère et vitesse d'approche « à l'infini » est par ailleurs très fréquente (et non moins regrettable), résultant sûrement du fait que la vitesse relative d'approche est celle qui détermine les caractéristiques de la trajectoire hyperbolique mais qu'il n'est pas facile d'expliquer cette notion de « vitesse à l'infini » pour un objet qui ne s'éloigne pas énormément de la Terre ! Alors, on la cite très souvent comme vitesse d'entrée dans l'atmosphère, sans tenir compte de l'accélération apportée par la Terre...

Quoi qu'il en soit, vous aurez remarqué que j'avais moi-même trouvé 19 km/s (vitesse d'approche à l'infini) comme la plus vraisemblable ! Et je reste par ailleurs persuadé que le groupe du SPMN devra aussi réviser à la baisse l'angle de descente du météore... Alors, l'ufologue français amateur d'orbites aurait-il été plus fort que les astronomes espagnols experts en météores qui sont sur place ? La réponse est clairement NON, mais j'ai sûrement eu eu beaucoup de chance.

Avec mes notions très superficielles dans ce domaine, je suis parti de l'hypothèse qu'un grand nombre d'astéroïdes susceptibles de heurter la Terre orbitent dans le même plan que celle-ci, et que la direction d'où ils proviennent, leur « radiant », serait donc généralement très proche de l'écliptique ; et j'ai cherché à faire « coller » au mieux la direction avec l'unique donnée exploitable dont je disposais, la vidéo tournée à León. Les experts espagnols, de leur côté, cherchaient précisément et sans a priori la direction du radiant d'après les témoignages, photographies et vidéos dont ils disposaient, et la difficulté est tout autre.

Ma supposition était plausible, mais pas réellement probable : un bon nombre d'astéroïdes suivent une orbite très proche de l'écliptique, mais pas aussi proche que je l'imaginais. La Terre elle-même peut d'ailleurs avoir été responsable de la déviation de leur orbite dans un passé plus ou moins lointain. On peut consulter les paramètres orbitaux de tous les « PHA » (potentially hazardous asteroids, astéroïdes potentiellement dangereux) connus sur un site de la NASA.

On constate qu'une bonne moitié de ces objets ont une orbite inclinée de moins de 10° sur l'écliptique. Mais 5 ou 10 degrés, c'est tout de même beaucoup, d'autant que cela peut modifier d'une valeur bien plus grande l'écart du radiant sur l'écliptique.

La météorite de Lost City

C'est ce que j'ai constaté en étudiant l'orbite, une des rares qui ait pu être reconstituée, de l'astéroïde responsabe le la météorite de Lost City, que le SPMN suspecte toujours d'être lié à celui qui nous intéresse...

Cette  météorite était tombé le 3 janvier 1970, pratiquement à la même date de l'année que celle d'Espagne. Il est donc tentant de penser qu'il s'agissait de deux objets suivant la même orbite, issus du même « corps parent », un astéroïde plus gros qui se serait fragmenté à la suite d'une collision.

Le cas s'est déjà présenté avec trois bolides ayant traversé quasi-simultanément le ciel de Bavière le 6 avril 2002, dont l'étude de la trajectoire a permis de montrer que l'objet responsable suivait la même orbite que celui d'où était issue la météorite tombée à  Pribram le 7 avril 1959 (la première météorite dont on a pu reconstituer l'orbite avant sa rencontre de la Terre). On peut lire l'histoire détaillée de cette découverte en français sur le site « Le monde des météorites ».

Voici donc les paramètres de l'orbite de la météorite de Lost City :

— demi-grand axe (SMA) = 1,661 UA (rayons d'orbite terrestre) ;
— excentricité = 0,417 ;
— inclinaison = 12° ;
— noeud ascendant = 283° ;
— argument du périhélie = 161°.

Et voici comment se présente cette orbite :


On sait calculer la vitesse de l'astéroïde au point de rencontre avec l'orbite terrestre :

V_A = √(2-D/SMA)×V_C.

D est ici le rayon terrestre et V_C la vitesse de la Terre, on aura donc :

V_A = √(2-1/1,661)×29,8 = 35,2 km/s.

La rencontre avec la Terre se situe au noeud descendant, c'est-à-dire lorsque l'objet passe sous l'écliptique. Ce qui signifie que cette orbite coupe celle de la Terre en descendant sous un angle de 12°.

On remarque aussi que le périhélie se situe très près du noeud descendant (dans les paramètres, il est à 161° du noeud ascendant, donc à 19° du noeud descendant), si bien que dans le plan de l'écliptique, la rencontre a lieu presque tangentiellement.

On peut donc considérer que le « triangle des vitesses » se situe dans un plan perpendiculaire à l'écliptique (il ne serait pas beaucoup plus difficile de faire les calculs dans les trois dimensions, mais quand on ne cherche pas une grande précision et qu'il est manifeste qu'on peut simplifier autant le faire) :


On trouve alors facilement la vitesse relative :

V_R = √((V_A×sinus a)²+(V_A×cosinus a -V_T)²) = √(V_A²+V_T²-2×V_T×V_A×cosinus a)
 = √(35,2²+29,8²-2×35,2×29,8×cosinus 12) = 8,7 km/s.

Et l'angle par rapport à l'horizontale :

b = arc sinus(V_A×sinus 12 /V_R) = 57,5°.

Cet angle correspond à l'écart du radiant par rapport à l'écliptique : avec une inclinaison d'orbite de 12°, on se retrouve avec un écart de presque 60° sur la sphère céleste ! C'est là qu'on se rend compte que mon hypothèse était assez restrictive (ceci dit, cette « amplification » résulte de la faible vitesse sur l'orbite concernée, assez inhabituelle).

On peut avec ces données estimer le radiant de l'orbite du météore de Lost City près de León : il suffit de chercher avec un logiciel d'astronomie le point situé à 57,5° perpendiculairement au cercle de l'écliptique vers le nord, et à 90° de la position du Soleil. Reporté sur la sphère céleste visible depuis les environs de la ville, ce point se trouve à 75° de hauteur sur l'horizon et 330° d'azimut (ça n'est qu'une approximation, je n'ai pas cherché à faire les calculs précis et j'espère juste ne pas m'être trompé).

Avec un azimut au nord-ouest et une telle hauteur sur l'horizon, ce radiant ne correspond absolument pas à celui du météore d'Espagne...

Mais cela n'interdit pas encore la possibilité que les deux objets aient le même corps parent : il n'est pas impossible que l'orbite du second ait été déviée par un passage à proximité de la Terre, peut-être justement lorsque le premier tombait dans l'Oklahoma en 1970... Dans ce cas, on aurait deux orbites différentes se coupant toutes les deux au même point de l'orbite terrestre. L'objet tombé en Espagne serait alors passé d'une orbite à l'autre en suivant une trajectoire hyperbolique à proximité de la Terre (c'est précisément ce qu'on appelle l'effet de fronde)...

Il reste donc à vérifier que cette trajectoire hyperbolique intermédiaire peut exister, et bien sûr que son périgée ne passe pas à l'intérieur du globe terrestre !

Nous avons vu que la direction des asymptotes d'une orbite hyperbolique correspond au déplacement relatif de l'astéroïde sur son orbite autour du Soleil... Notre orbite hyperbolique « de transition » devrait avoir une de ses asymptotes dans la direction d'approche d'une des orbites, et l'autre dans la direction opposée à celle d'approche de l'autre orbite... Si je n'ai pas été très clair, ce petit schéma vous aidera à comprendre :


Et une autre nécessité est que les deux vitesses soient identiques. Or, nous venons de voir que la vitesse d'approche sur l'orbite « Lost City » est de 8,7 km/s, alors que celle du météore d'Espagne est estimée à 19±3 km/s (ou 15±4 si la vitesse indiquée est celle d'entrée dans l'atmosphère ; ça serait encore trop)... Un tel écart exclut totalement, sauf grosse erreur de ma part, tout lien de « parenté » entre les deux météore.

La suite appartient aux spécialistes

Quoi qu'il en soit, on constate que ma supposition d'un radiant situé précisément sur l'écliptique n'a quelque valeur que pour des astéroïdes dont l'orbite ne s'écarte pas de plus d'un ou deux degrés de l'écliptique... Et de tels astéroïdes sont assez nombreux comme on peut le voir sur la liste des PHE établie pas la NASA, mais pas majoritaires. Si la trajectoire que j'ai estimée devait se confirmer, ça ne serait donc rien de plus qu'un coup de chance !

Ceci dit, nous avons vu que les orbites de quelques astéroïdes seulement ont pu être reconstituées (six avec précision, et une dizaine de plus de façon approximative). Dans chaque cas, cela a été possible grâce à des réseaux d'enregistrements photographiques ou vidéo mis en place spécialement pour cela... Les photographies de nuit sont particulièrement utiles dans ce domaine, puisqu'elles permettent de repérer très précisément la trajectoire du météore par rapport aux étoiles.

Avec le météore du 4 janvier, on n'a pas cette chance, mais la présence de la Lune sur la vidéo de León est déjà un élément inespéré... Les chercheurs espagnols du SPMN disposent en outre de plusieurs photographies qui n'ont pas été diffusés, et cherchent en combinant tout cela à reconstituer très précisément la trajectoire. C'est un travail de longue haleine, nécessitant des reconstitutions précises de toutes les photographies et de la vidéo pour en extraire des données angulaires exactes, et ensuite beaucoup de calculs... Bref, les approximations et suppositions diverses que je me suis permises dans mon approche toute théorique d'initiation aux calculs orbitaux n'ont aucune place dans une telle recherche.

Au passage, je me suis rendu compte qu'il y avait dans la vidéo un autre moyen « d'étalonner » (approximativement toujours) les dimensions angulaires que celui que j'ai utilisé, et cette fois verticalement : on sait en effet que la lune, visible sur la vidéo, se trouvait à 22,6° de l'horizontale, et la position horizontale approximative peut être déduite de la séquence finale, quand le vidéaste filme un spectacle au sol. C'est la hauteur à laquelle on doit retrouver le visage (en fait un peu plus haut, le vidéaste tenant apparemment son caméscope au-dessus de sa tête) d'autres personnes (pas les personnages au premier plan, qui sont sur une estrade, mais on en voit d'autres plus loin) :


Cela me conduit à réviser légèrement à la hausse mon estimation précédente : l'angle que j'estimais à 30 degrés doit plutôt représenter 33 degrés, et de ce fait ma « grille de repérage » doit être rétrécie de 10% (ceci dit, si je n'ai fait que dix pour cent d'erreur, se rerai très satisfait). Ça ne change pas grand- chose, la marge d'erreur reste de toute façon trop grande pour faire du travail vraiment sérieux de reconstitution de trajectoire.

Les chercheurs espagnols ont de leur côté bon espoir d'arriver à une précision suffisante pour déduire les caractéristiques de l'orbite, ce qui serait je crois une première pour un météore observé de jour... On peut leur faire confiance en tout cas pour tirer le maximum des documents dont ils disposent.

Attendons donc leurs résultats définitifs, sans nous montrer impatients...

Additif (27/01/2004)

Il y a bien eu des témoins en France

Comme je m'en doutais, le météore d'Espagne a aussi été obsevé en France. Cet article de la Nouvelle République des Pyrénées du 8 janvier, qui nous a été aimablement transmis par notre correspondante Agnès, détaille deux témoignages de la région de Lannemezan, particulièrement intéressants car précis.


Le premier témoin dit que l'objet « venait du sud-ouest et montait du ciel », et « traçait une hyperbole venant vers nous et se dirigeant vers le nord-est. »

On peut le féliciter pour son appréciation d'une trajectoire hyperbolique, mais ce qui nous interpelle c'est la mention de « montée du ciel ». Cela confirme sûrement que le météore descendait suivant un angle assez faible par rapport à l'horizontale. S'il était passé de 80 à 30 km d'altitude en quelque 70 km comme l'indiquent (en mentionnant bien toutefois qu'il s'agit d'une appréciation provisoire) les chercheurs espagnols du SPMN, sa trajectoire apparente aurait été continuellement et franchement descendante pour un observateur de Lannemezan.

Notons que Lannemezan se trouve à près de 500 km de León. Théoriquement, on peut voir à une telle distance un objet à 19 km d'altitude. Mais la chaîne des Pyrénées, qui se dresse à une hauteur angulaire d'à peu près 1° dans cette direction, implique en fait une altitude supérieure à 25 km. C'est un peu moins que celle que nous avons estimée, le météore a donc dû disparaître alors qu'il se situait à proximité de cette ville. Quant à son apparition, elle dépend surtout du moment où il est devenu visible.

Nouvelle feuille de calcul

Il reste à savoir si la trajectoire pouvait vraiment être montante au début... Pour le savoir, j'ai créé une nouvelle feuille de calcul, plus étendue que la première... Ceux que la partie théorique n'intéresse pas et qui ignorent tout des tableurs peuvent encore la sauter.

D'abord, puisqu'il m'est apparu que mon hypothèse de base d'un radiant (direction d'origine sur la sphère céleste) était sûrement très (trop) approximative, j'ai étendu les calculs aux autres cas possibles... Autant dire qu'avec les données très fragmentaires dont nous disposons on pourra trouver de nombreuses trajectoires différentes... Mais encore une fois, mon but n'est pas d'essayer de faire mieux que les spécialistes qui s'occupent de l'affaire sur place, mais juste de donner quelques notions sur les méthodes que l'on peut employer.

La première variable que l'on peut modifier est le cap suivi. Le tableur ajuste ensuite automatiquement l'angle de descente pour qu'il corresponde à l'angle apparent sur la vidéo (que j'ai un peu corrigé au passage : 55,5° au lieu de 56,6)...

On peut ensuite changer la vitesse théorique (le freinage par le frottement atmosphérique n'est toujours pas pris en compte) du météore... Il s'agit de la vitesse au niveau du point de référence, et la vitesse à l'infini s'ajuste automatiquement, de même que la vitesse angulaire en azimut correspondante sur la vidéo. Il est bien sûr toujours nécessaire que cette dernière soit supérieure à celle qui a été mesurée, l'objet ayant été freiné par l'atmosphère... Si ça n'est pas le cas, on doit diminuer l'altitude du point de référence, ce qui rapproche la trajectoire de León.

Si on veut s'amuser à essayer de reconstituer l'orbite théorique à partir de ces données, on dispose de la direction du radiant : azimut et hauteur sur l'horizon... Il reste à faire le conversion en coordonnées par rapport à l'écliptique à l'aide d'un logiciel d'astronomie, correspondant à la direction d'arrivée du météore « à l'infini », c'est-à-dire avant qu'il ne subisse de façon sensible l'influence de la Terre.

Avec cela, il est toujours possible de déduire la vitesse de l'objet sur son orbite, et par là de reconstituer cette orbite complète, y compris cette fois l'inclinaison par rapport à l'écliptique. Je n'ai pas placé les calculs correspondants sur la feuille, parce que l'orbite ainsi calculée n'aurait sûrement aucun rapport avec la réalité et que dans quelques heures je pars à vélo au Festival Science-frontières, mais ça n'est pas beaucoup plus compliqué que ceux que j'avais placés dans la feuille de calcul précédente pour des calculs en deux dimensions, sur le plan de l'écliptique.

Le principal ajout consiste en indications concernant la trajectoire de 50 en 50 km : en particulier l'altitude et les coordonnées géographiques du point survolé...

Et surtout, le tableur calcule pour ces différentes positions la trajectoire apparente de l'objet vu depuis un lieu particulier : Lannemezan par défaut, ville près de la quelle se trouvait notre témoin, mais vous pouvez changer en introduisant les coordonnées géographiques et l'altitude du lieu de votre choix.

On trouve ainsi l'azimut (direction d'observation), la distance de l'objet, sa hauteur angulaire (par rapport à l'horizontale, ne pas oublier que les Pyrénées peuvent augmenter un peu la hauteur de l'horizon), et l'angle de descente apparent.

Ainsi, on peut savoir immédiatement si une trajectoire est compatible avec une observation depuis un point particulier, et simuler toutes les caractéristiques de l'observation.

On peut aussi régler ainsi les paramètres pour obtenir un passage à la verticale d'un point géographique particulier... Malheureusement, je ne connais pas de point dont on soit sûr qu'il a été survolé à la verticale, mais les enquêteurs espagnols en ont certainement recueilli.

Conclusion concernant ce témoignage

Et on peut aussi savoir si, depuis les environs de Lannemezan, la trajectoire a pu être montante comme notre témoin l'indique.

La réponse est oui, mais dans des conditions très particulières et pour tout dire douteuses : il faut que l'angle de descente du météore soit très faible, ce que l'on obtient en réglant le cap à un peu plus de 55°. Mais la « montée » suit un angle extrêmement faible, et la hauteur angulaire permet à peine de voir l'objet au-dessus des Pyrénées. Il me semble préférable de considérer des conditions moins extrêmes, en remarquant que le témoin roulant sur l'autoroute n'était pas particulièrement bien placé pour apprécier précisément l'horizontale.

On peut tout de même obtenir en jouant un peu sur les différents paramètres un angle de descente faible au début de l'observation, et qui augmente sensiblement en quelques secondes. Notons qu'une vitesse faible tend à augmenter l'amplitude de cette variation.

Tout cela ne change pas grand-chose à nos précédentes estimations : je suis tenté de donner un cap compris près de León entre 51 et 56°, un angle de descente entre 8 et 13°, et une vitesse « à l'infini » entre 9 et 16 km/s (un peu inférieure à mon estimation précédente)...

Notons au sujet de la vitesse qu'il n'est pas exclu avec ces nouvelles considérations qu'elle soit identique à celle du météore de Lost City (8,7 km/s). Mais je suppose que le groupe du SPMN qui dispose de bien plus de données a de bonnes raisons de donner une vitesse comprise entre 16 et 22 km/s (ou entre 11 et 19 s'il parle de la vitesse d'entrée dans l'atmosphère). Je tends donc à privilégier de l'ordre de 16.

Le second témoignage n'apporte pas grand-chose, sinon une indication sur la durée (4 ou 5 secondes au maximum), qui n'est de toute façon jamais très fiable.

Un expert toujours égal à lui-même

L'article du journal mentionne aussi les commentaires d'un « expert » français... Sans surprise, il s'agit de l'incontournable Jean-Jacques Velasco !

Son opinion : « Cela correspond très probablement au phénomène observé en Espagne et au Portugal et qui a aussi été vu à Cestas, en Gironde ».

Encore un témoignage en France donc, et le SEPRA en a sûrement collecté d'autres, avec son statut de service d'expertise officiel... Ça pourrait profiter à de véritables chercheurs qui seraient capables de les exploiter, mais comme d'habitude le chef du SEPRA les gardera pour lui sans rien en faire, et jouera de son influence pour empêcher les autres de faire ce dont lui-même est incapable...

Que le météore ait été vu à Cestas ne nous apprend rien si on n'a aucune donnée angulaire : quel que soit le choix de la trajectoire, il est toujours bien visible depuis Cestas, sous un angle qui passe très à l'est des Pyrénées.

Continuons :

Mais un détail interpelle cependant l'expert :
« Si l'heure est la même, la direction du phénomène observé dans les Pyrénées ne me semble pas la bonne par rapport au bolide tombé en Espagne, elle est d'ailleurs plutôt à l'inverse. »

Le 7 janvier, quand Velasco a déclaré cela, tous ceux qui s'intéressaient aux météores savaient que la direction annoncée initialement dans la presse était fausse, et correspondait à un alignement fortuit des témoignages.

Ainsi, dès le 6 au matin, on trouvait sur la liste Meteorobs un courrier indiquant que la trajectoire suivait une direction nord-est. L'information était immédiatement reprise par d'autres listes consacrées aux météores aussi bien qu'aux satellites ou à des sujets plus généraux, ainsi que bon nombre de sites s'occupant de ce phénomène.

Mais le 7, notre expert national, lui, n'avait rien lu d'autre que les dépêches de presse du 5.

Et le fait que les deux témoignages cités dans le journal (et combien d'autres qu'il avait recueillis par son statut privilégié ?) indiquaient clairement une trajectoire pratiquement à l'opposé de celle qu'il imaginait ne l'émeuvait pas outre mesure :

Néanmoins, pour avoir travaillé depuis des années sur ce type d'observations et de témoignages, cela ne le surprend pas forcément : « La vision stéréoscopique de l'homme permettant d'évaluer une distance s'arrête à 40 mètres. Au delà, si aucun élément extérieur ne donne l'échelle de référence, on ne peut estimer une distance et régulièrement, aussi, sur un même phénomène de chute de météorite, on note des écarts dans les témoignages sur les trajectoires pouvant varier jusqu'à 180° » relève-t-il.

En quoi la vision stéréoscopique intervient-elle pour apprécier des directions ? Bien sûr, si on recueille 500 témoignages concernant un même phénomène, il s'en trouvera toujours deux ou trois qui donneront une direction totalement à l'opposé de la réalité... Mais quand les deux seuls témoins, indépendants, dont on dispose font cette même « erreur », on peut se douter que quelque chose cloche !

Mais il est vrai que Velasco, pour avoir « travaillé depuis des années sur ce type d'observations et de témoignages », trouve sûrement un grand nombre de témoins « qui se trompent » quand lui-même annonce dans une de ses fabuleuses « expertises » une trajectoire totalement fausse : effectivement, le 5 novembre 1990, une grande proportion de témoins parmi les centaines ayant déposé à la gendarmerie disaient avoir vu un phénomène lumineux passer de gauche à droite alors que d'après la trajectoire de la rentrée atmosphérique annoncée, et toujours pas démentie, par le SEPRA ç'aurait dû être de droite à gauche !

En bref, notre expert est toujours égal à lui-même, et il semble donc qu'il soit toujours présenté comme expert dans le domaine des rentrées atmosphériques, même si on a jugé bon de ne plus l'indiquer dans l'intitulé de l'organisme qu'il dirige.

Et moi qui ne suis pas expert mais qui dépense beaucoup de temps pour essayer de donner des informations fiables sur les rentrées atmosphériques et les météores, bref qui fais bénévolement le travail pour lequel il est grassement payé et qu'il n'a jamais fait, j'ai dû en plus lui verser près de 4000 euros (toutes mes économies, et je lui en dois encore, il pourrait bien mettre un terme définitif à mes activités qui le dérangent en saisissant mon matériel informatique, puisque c'est tout ce qui me reste) parce que j'ai osé écrire qu'il était une nullité absolue dans le domaine des rentrées atmosphériques ! J'ai largement démontré que TOUT ce qu'il avait fait dans ce domaine en dénotait la méconnaissance la plus totale, sans la moindre exagération, et rien de ce que j'ai écrit n'a été démenti, mais il a réussi à me faire condamner en s'attirant par on ne sait quels procédés la complicité du Procureur général de la Cour d'appel d'Aix-en-Provence... L'affaire est maintenant en Cassation, et semble bien partie pour être tout aussi truquée qu'en appel...

Excusez-moi de vous avoir encore imposé une petitre diatribe contre le SEPRA, mais si personne ne veut parler de cette affaire je risque fort de ne bientôt plus pouvoir écrire du tout... Pour ne pas terminer sur cette note déplaisante, je rappelle les principaux sites sur lesquels vous pourrez trouver d'autres informations relatives au météore du 4 janvier. De mon côté, je ne pense pas reparler de cette affaire avant que des résultats définitifs ne soient annoncés par les scientifiques qui s'en occupent (et qui n'ont vraiment rien de commun avec le « service d'expertise » français !)

Le principal est celui du Spanish fireball network (SPMN), qui a pris en main l'étude précise de la trajectoire et qui en tirera sûrement des données scientifiques passionnantes. La page consacrée à l'événement qui nous intéresse est mise à jour très souvent :

Red de Investigación Sobre Bólidos y Meteoritos (SPMN) (textes en espagnol et en anglais).

Deux autres sites espagnols apportent des informations intéressantes sur cette affaire :
Sociedad de Observadores de Meteoros y Cometas de España (SOMYCE) ;
InfoAstro.

Et aussi un site allemand en anglais, qui cite tous les liens importants se rapportant à l'affaire :
Dutch Meteor Society.

Robert Alessandri

Deuxième partie

---